Verschieben von Funktionsgraphen: Unterschied zwischen den Versionen

Version vom 22. Mai 2013, 20:14 Uhr

Wiederholung: Verschiebung von Parabeln

Du weißt bereits, wie sich Parameter auf die Graphen von Parabeln auswirken können.

Im folgenden Applet kannst du über die Funktionen h bzw. g die Verschiebung nach links/rechts (durch den Schieberegler a) bzw. nach oben/unten (durch den Schieberegler b) beobachten.
Klicke auf die jeweiligen Checkboxen im Applet, um die Funktionen anzuzeigen oder auszublenden.

In der Funktion j werden beide Arten der Verschiebung zusammengeführt.

Auch andere Funktionsgraphen lassen sich derartig verschieben.
Im folgenden wollen wir untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.
Fülle parallel zum Lernpfad das Arbeitsblatt aus, auf dem alle wichtigen Informationen zusammengefasst werden:

Verschiebung nach links/rechts

Fülle den ersten Abschnitt auf deinem Arbeitsblatt aus:

Vergleiche die beiden Graphen an den vorgegebenen Werten: h(1,5) = -3,375 = f (-1,5) = f (1,5 - ____) h(3) = _____ = f (___) = f (_____ - _____) h(4) = ____________________________________________ Wie lässt sich h(x) aus f (x) herleiten? -> h(x) = _________________________________________ Für jeden x - Wert ist der Funktionswert von h gleich dem Funktionswert von f an der Stelle __________.

Vergleiche deine Antworten mit der Lösung und bessere gegebenenfalls aus:

Allgemein

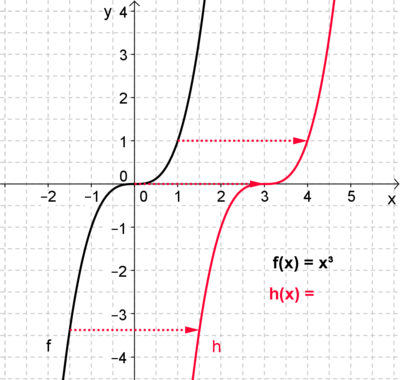
Im folgenden Applet ist die ganzrationale Funktion f: x -> x³ in schwarzer Farbe abgebildet.
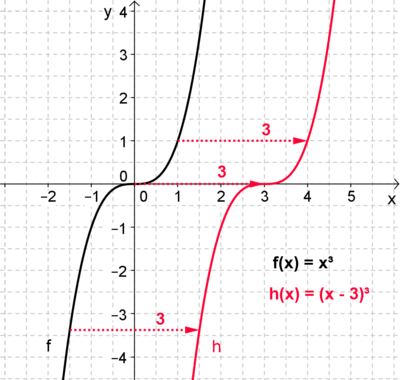
Verschiebe den roten Graphen der Funktion h: x -> (x - a)³, indem du über den Schieberegler den Parameter a veränderst.

Welche Auswirkungen hat eine Veränderung von a auf den Graphen von h?
Was passiert, wenn a kleiner bzw. größer wird?
In welche Richtung wird der Graph von h verschoben, wenn a negativ bzw. positiv ist?

Vergleiche dazu die Wertetabelle!

Verschiebung nach oben/unten

Bearbeite nun den zweiten Abschnitt auf dem Arbeitsblatt:

Vergleiche auch hier die beiden Graphen bei: g(-1,5) = -1,375 = f (-1,5) + ____ g(0) = ______ = f (___) + ____ g(1) = _____________________________ Welcher Zusammenhang besteht zwischen den beiden Funktionen? -> g(x) = f ( ______ ) _______ Für jeden x-Wert ist der Funktionswert von g gleich dem Funktionswert von f an der Stelle ________.

Kontrolliere dein Ergebnis mit den versteckten Lösungen:

Allgemein

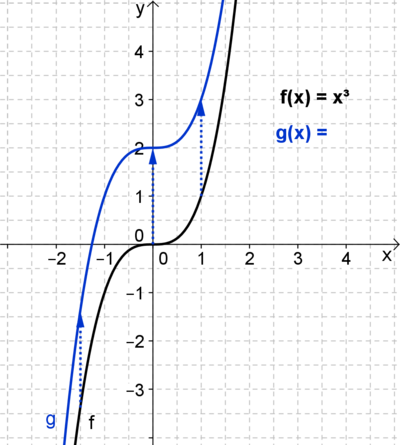
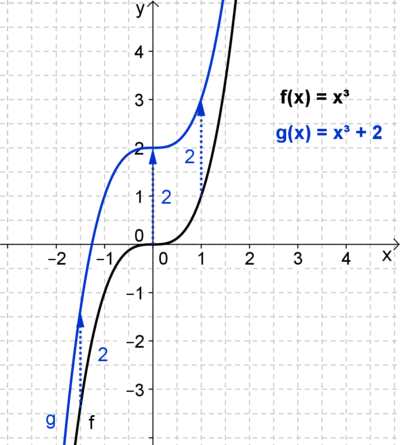
Die Funktion g: x -> x³ + b lässt sich mittels des Parameters b nach oben und unten verschieben.
Wenn du den Schieberegler auf b = 2 einstellst, erhälst du die obige Funktion g: x -> x³ + 2.

Wie wirkt sich die Veränderung des Parameters b auf den Graphen von g aus?
Was bewirkt ein positiver bzw. ein negativer Parameter b?

Beachte auch hier die Wertetabelle!

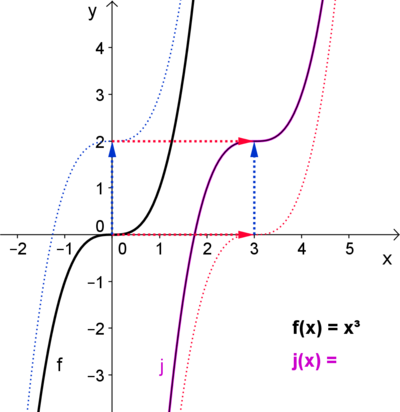
Kannst du die folgenden Graphen und Funktionsterme richtig zuordnen?

	f(x) = 3x³ + 1
	g(x) = x + 3
	h(x) = x² - 3
	j(x) = x³ + 5
	k(x) = x⁴ - 2

Verschiebung nach links/rechts und oben/unten

Jetzt widme dich dem dritten Abschnitt auf dem Arbeitsblatt!

Die Funktion j entsteht aus der Funktion f, die um ________________ nach rechts und _________________ nach oben verschoben wird. Vergleiche die beiden Graphen in einem charakteristischen Punkt: j (3) = ____ = f (0) ______ = f (___ - ___) + ___ Im Funktionsterm von j äußert sich die Verschiebung wie folgt: -> j (x) = f ( __________)__________ Für jeden x-Wert ist der Funktionswert von j gleich dem Funktionswert f (_____________).

Dein Ergebnis kannst du hier überprüfen:

Allgemein

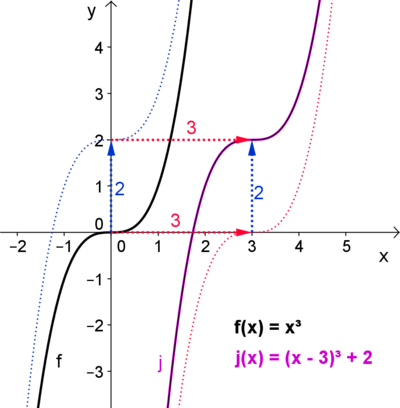
In der Funktion j: x -> (x - a)³ + b werden beide Möglichkeiten der Verschiebung zusammengeführt.

Wie wirkt sich die Veränderung von a und b auf den Graphen der Funktion j aus?

Kannst du eine allgemeine Regel aufstellen?

Fülle den Lückentext mit den vorgegebenen Antwortmöglichkeiten aus.
Ergänze anschließend die Lücken im Merksatz auf deinem Arbeitsblatt.