Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Testseite: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Ein Besuch im | + | ==Ein Besuch im Zoologischen Garten== |
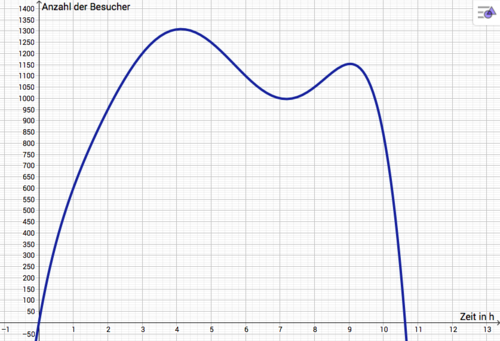
| − | Auf der Kursfahrt in Berlin besucht ihr den Zoologischen Garten | + | Auf der Kursfahrt in Berlin besucht ihr den Zoologischen Garten, der von 9:00 bis 19:45 Uhr geöffnet ist. Vor dem Ausflug schaut ihr euch die Besucherzahlen an, die zuvor ermittelt wurden. Der folgende Graph beschreibt die Anzahl der Besucher in Abhängigkeit von der Zeit in Stunden im Intervall [0;10,6]. |
::: [[Datei: Besucher Zoo Graph.png|rahmenlos|500px|Fläche 1]] | ::: [[Datei: Besucher Zoo Graph.png|rahmenlos|500px|Fläche 1]] | ||
| + | |||
| + | Die folgende Wertetabellle gibt die genauen Daten an: | ||
{| border="1" cellspacing="0" valign="top" | {| border="1" cellspacing="0" valign="top" | ||
| Zeile 38: | Zeile 40: | ||
{{Aufgabe|}} | {{Aufgabe|}} | ||
| − | <iframe src="https://learningapps.org/watch?v= | + | <iframe src="https://learningapps.org/watch?v=pq8bxyutv17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| Zeile 73: | Zeile 75: | ||
| − | {{Aufgabe|In der folgenden | + | {{Aufgabe|In der folgenden Abbildung siehst du den Punkt P auf dem zuvor eingeführten Graphen und eine rote Gerade. |
| − | <iframe scrolling="no" title="Graph Besucher Zoo" src="https://www.geogebra.org/material/iframe/id/Ab6qkqg3/width/ | + | |
| + | <iframe scrolling="no" title="Graph Besucher Zoo" src="https://www.geogebra.org/material/iframe/id/Ab6qkqg3/width/800/height/600/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false" width="800px" height="600px" style="border:0px;"> </iframe> | ||
| Zeile 90: | Zeile 93: | ||
Brauchst du Hilfe? Dann klicke hier: | Brauchst du Hilfe? Dann klicke hier: | ||
<popup name="Hilfe"> | <popup name="Hilfe"> | ||
| − | Gehe zu der Aufgabe "Was sind nochmal Differenzen- und Differenzialquotient?" zurück. Dort bekommst du einen guten Überblick über die verschiedenen | + | Gehe zu der Aufgabe "Was sind nochmal Differenzen- und Differenzialquotient?" zurück. Dort bekommst du einen guten Überblick über die verschiedenen Änderungsraten und darüber, was sie explizit bedeuten. Überlege dir also, welche Änderungsrate du für diese Aufgabe benötigst und stelle eine Verbindung zur Tangente her. |
</popup> | </popup> | ||
Vergleiche deine Lösung hier: | Vergleiche deine Lösung hier: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | Die Steigung der Tangente am Graphen im Punkt P(x|y) ist gleich der momentanen Änderungsrate von dem Graphen an der Stelle x vom Punkt P. Indem du also m kennst, kannst du bestimmen, um wie viel sich die Anzahl der Besucher zum Zeitpunkt x (d. h. zu einer bestimmten Uhrzeit) verändert. | + | Die Steigung der Tangente am Graphen im Punkt P(x|y) ist gleich der momentanen Änderungsrate von dem Graphen an der Stelle x vom Punkt P. Indem du also die Tangentensteigung (also m) kennst, kannst du bestimmen, um wie viel sich die Anzahl der Besucher zum Zeitpunkt x (d. h. zu einer bestimmten Uhrzeit) verändert. |
| − | + | ||
</popup> | </popup> | ||
| − | |||
}} | }} | ||
| + | {{Aufgabe|}} | ||
| + | <iframe src="https://learningapps.org/watch?v=p1wzdxb5k17" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
Aktuelle Version vom 23. Oktober 2017, 10:38 Uhr
Ein Besuch im Zoologischen Garten
Auf der Kursfahrt in Berlin besucht ihr den Zoologischen Garten, der von 9:00 bis 19:45 Uhr geöffnet ist. Vor dem Ausflug schaut ihr euch die Besucherzahlen an, die zuvor ermittelt wurden. Der folgende Graph beschreibt die Anzahl der Besucher in Abhängigkeit von der Zeit in Stunden im Intervall [0;10,6].
Die folgende Wertetabellle gibt die genauen Daten an:
| Zeit in Stunden nach Öffnung des Zoos | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 10,6 |
| Anzahl der Besucher | 0 | 600 | 950 | 1200 | 1308 | 1249 | 1100 | 1000 | 1050 | 1151 | 837 | 0 |
|
In welchem Zeitraum nimmt die Besucherzahl ab bzw. zu? Ermittle die Zeitintervalle durch ungefähres Ablesen der Punkte am Graphen. Notiere die Lösung in deinen Ordner. Brauchst du Hilfe? Dann klicke hier: Vergleiche deine Lösung hier:
Brauchst du Hilfe? Dann klicke hier: Vergleiche deine Lösung hier:
|
|
In der folgenden Abbildung siehst du den Punkt P auf dem zuvor eingeführten Graphen und eine rote Gerade.
Vergleiche deine Lösung hier:
Brauchst du Hilfe? Dann klicke hier: Vergleiche deine Lösung hier: |