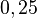Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Rechnen mit rationalen Zahlen: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 1: | Zeile 1: | ||
==== <u>'''Was sind Rationale Zahlen?'''</u> ==== | ==== <u>'''Was sind Rationale Zahlen?'''</u> ==== | ||
| − | Unter Rationalen Zahlen versteht man alle | + | Unter Rationalen Zahlen versteht man alle euch bereits bekannten "ganzen Zahlen" (N) |
Zu den Rationalen Zahlen (Q) gehören jetzt aber außerdem noch Brüche und Dezimalzahlen. | Zu den Rationalen Zahlen (Q) gehören jetzt aber außerdem noch Brüche und Dezimalzahlen. | ||
| − | <span style="color: #B452CD">Bsp. zu Brüchen: </span> <math>\frac{ | + | <span style="color: #B452CD">Bsp. zu Brüchen: </span> <math>\frac{1}{2}</math> oder <math>3</math> <math>\frac{3}{6}</math> |
| − | <span style="color: #B452CD">Bsp. zu Dezimalzahlen:</span> < | + | <span style="color: #B452CD">Bsp. zu Dezimalzahlen:</span> <math>2,5</math> oder <math>-9,1</math> |
| + | |||
| + | |||
| + | === '''1. Die Menge der Rationalen Zahlen''' === | ||
| + | |||
| + | grafik! | ||
| + | |||
| + | Beachte: Die Divion mit Rationalen Zahlen ist nun auch möglich, auch wenn der Dividend kein ganzzahliges Vielfaches des Divisors ist. Durch Die Zahl 0 darf jedoch immer noch nicht dividiert werden! | ||
| + | |||
| + | Verschiedene Schreibweisen: <math>\frac{1}{4}</math> = <math>0,25</math> | ||
Version vom 23. November 2017, 14:35 Uhr
Was sind Rationale Zahlen?
Unter Rationalen Zahlen versteht man alle euch bereits bekannten "ganzen Zahlen" (N)
Zu den Rationalen Zahlen (Q) gehören jetzt aber außerdem noch Brüche und Dezimalzahlen.
Bsp. zu Brüchen:  oder
oder 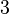

Bsp. zu Dezimalzahlen: 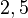 oder
oder 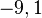
1. Die Menge der Rationalen Zahlen
grafik!
Beachte: Die Divion mit Rationalen Zahlen ist nun auch möglich, auch wenn der Dividend kein ganzzahliges Vielfaches des Divisors ist. Durch Die Zahl 0 darf jedoch immer noch nicht dividiert werden!
Verschiedene Schreibweisen:  =
=