Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Kehrsatz: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 18: | Zeile 18: | ||
==== Für Interessierte: Beweis des Kehrsatzes ==== | ==== Für Interessierte: Beweis des Kehrsatzes ==== | ||
| − | |||
{| border="0" | {| border="0" | ||
! style="width:40%"| | ! style="width:40%"| | ||
| Zeile 36: | Zeile 35: | ||
| [[Datei:Rechtwinkliges Dreieck.JPG|400px]] | | [[Datei:Rechtwinkliges Dreieck.JPG|400px]] | ||
|} | |} | ||
| − | |||
<br /> | <br /> | ||
Version vom 6. Juli 2018, 13:39 Uhr
Arbeitsaufträge:
- Schaue dir das Videos an, wie die Umkehrung des Satzes von Thales lautet.
- Beantworte die Kontrollfrage.
- Notiere dir, anhand der vorgegeben Fragen, Bemerkungen in OneNote.
- Erstelle einen Hefteintrag in deinem Skript.
Inhaltsverzeichnis |
Kehrsatz zum Satz des Thales
Merke: Umkehrung des Satzes von Thales
Wenn ein Dreieck bei C einen rechten Winkel hat, dann liegt die Ecke C dieses Dreiecks auf dem Halbkreis über [AB].
Für Interessierte: Beweis des Kehrsatzes
Kontrollfrage
Quellenangabe
Video "Rechtwinklige Dreiecke - Satz des Thales (Teil 1)" von Mathegym, über https://www.youtube.com/watch?v=RGZs_R7YFgE (Zugriff am 28.05.2018)
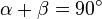 .
.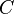 lässt sich daher eine Gerade
lässt sich daher eine Gerade 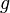 so legen, dass
so legen, dass 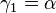
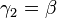
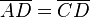 und
und 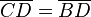 .
.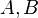 und
und 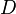 entfernt, liegen somit auf dem Kreis um
entfernt, liegen somit auf dem Kreis um ![[AB]](/images/math/5/e/3/5e32d4dbe98ef3af1b5123ccba43cbf7.png) ist.
ist.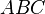 bei
bei