Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Graphisches Ableiten: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
| − | * Wenn dir das Thema noch Schwierigkeiten bereitet, beginne mit den Förderaufgaben ( | + | * Wenn dir das Thema noch Schwierigkeiten bereitet, beginne mit den Förderaufgaben (Aufgabe 1 bis Aufgabe 3). |
| − | * Wenn du dich bereits sicher fühlst, probiere die Forderaufgaben ( | + | * Wenn du dich bereits sicher fühlst, probiere die Forderaufgaben (Aufgabe 3 Aufgabe 5). |
| Zeile 18: | Zeile 18: | ||
| − | == Aufgabe 2 == | + | == Aufgabe 2 (Förderaufgabe) == |
<iframe src="https://learningapps.org/watch?app=5695909" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?app=5695909" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| Zeile 29: | Zeile 29: | ||
<popup name="Hilfestellung 1000000">Denke an notwendige und hinreichende Bedingungen einer Wendestelle</popup> | <popup name="Hilfestellung 1000000">Denke an notwendige und hinreichende Bedingungen einer Wendestelle</popup> | ||
| − | == Aufgabe 3 == | + | == Aufgabe 3 (Förder- & Forderaufgabe) == |
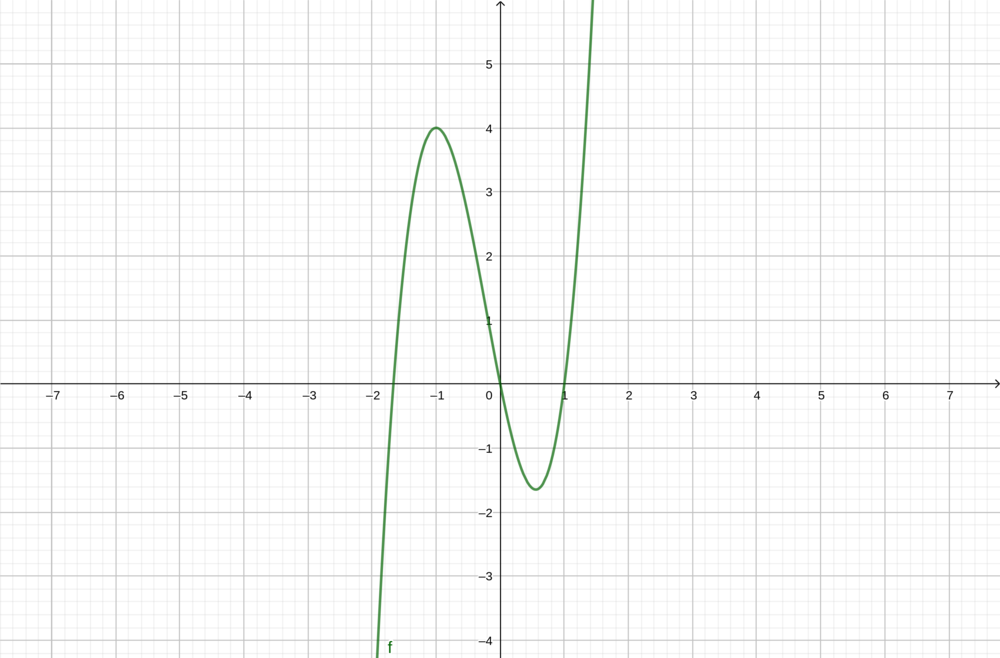
[[Datei:Aufgabe 3.png|f(x)=5x^(4)+3x^(3)-4x^(2)|1000px|links|rahmenlos]]<br /> | [[Datei:Aufgabe 3.png|f(x)=5x^(4)+3x^(3)-4x^(2)|1000px|links|rahmenlos]]<br /> | ||
| Zeile 141: | Zeile 141: | ||
| − | <popup name="Hilfestellung 1">Was sagt die Nullstelle | + | <popup name="Hilfestellung 1">Was sagt die Nullstelle einer Ableitung über ihre Stammfunktion aus?</popup> |
| − | <popup name="Hilfestellung 2"></popup> | + | <popup name="Hilfestellung 2">Was bedeuten negative Funktionswerte der Ableitungsfunktion für ihre Stammfunktion? Was positive Funktionswerte?</popup> |
| − | <popup name="Hilfestellung 3"></popup> | + | <popup name="Hilfestellung 3">Liegt eine Nullstelle in der Ableitung vor, hat die Stammfunktion hier eine Extremstelle. Verläuft die Ableitungsfunktion unterhalb der x-Achse, so fällt die Stammfunktion auf diesem Intervall. Für einen Verlauf oberhalb der x-Achse steigt die Stammfunktion.</popup> |
== Aufgabe 5 (Forderaufgabe) == | == Aufgabe 5 (Forderaufgabe) == | ||
Version vom 14. Oktober 2018, 17:16 Uhr
Bei einer Kurvendiskussion werden markante Punkte gesucht, die uns Auskunft über die Eigenschaften einer Funktion geben. Das wichtigste Hilfsmittel ist dabei die Ableitung. Kenntnisse über den Zusammenhang einer Funktion und ihrer Ableitung sind daher grundlegend für die Analysis. In diesem Lernpfad kannst du üben, Funktionen und ihre Ableitungen anhand ihrer Graphen zu untersuchen. Im Folgenden findest du Aufgaben um deine Kenntnisse im graphischen Ableiten zu vertiefen (Forderaufgaben) aber auch um Lücken zu schließen und Stoff zu wiederholen (Förderaufgaben). Unter jeder Aufgabe gibt es Hilfestellungen, auf die du zurückgreifen kannst, wenn du mal nicht weiterkommst.
- Wenn dir das Thema noch Schwierigkeiten bereitet, beginne mit den Förderaufgaben (Aufgabe 1 bis Aufgabe 3).
- Wenn du dich bereits sicher fühlst, probiere die Forderaufgaben (Aufgabe 3 Aufgabe 5).
Inhaltsverzeichnis |
Aufgabe 1 (Förderaufgabe)
Ordne den Graphen der Funktionen f(x) die richtigen Ableitungen zu.
Aufgabe 2 (Förderaufgabe)
Aufgabe 3 (Förder- & Forderaufgabe)
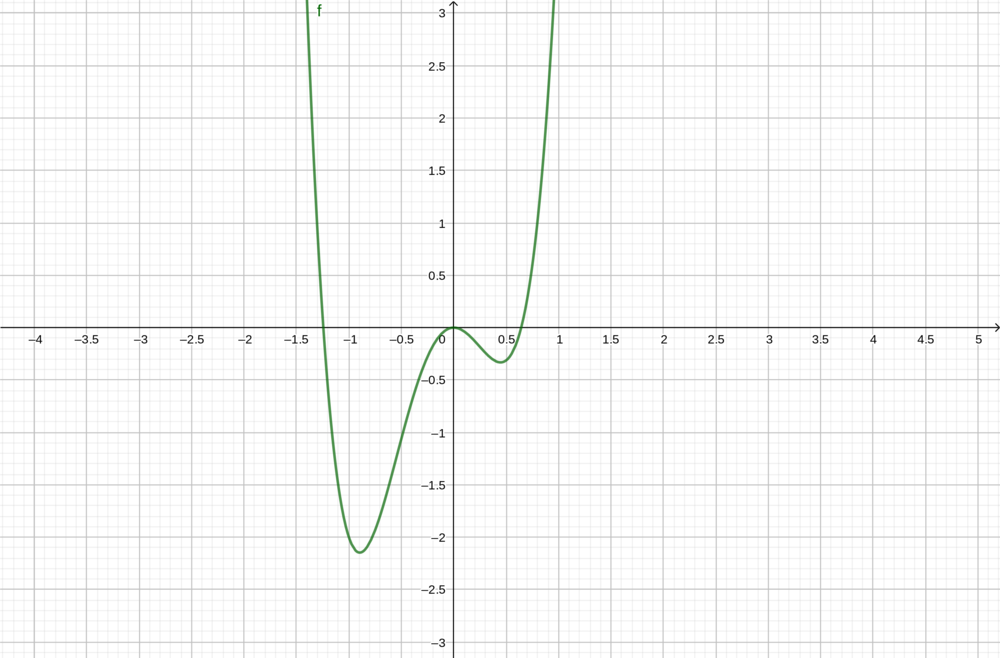
Aufgabe 4 (Forderaufgabe)
Die Abbildung zeigt den Graphen einer Funktion f'(x). Skizziere die dazugehörige Funktion f(x) in deinem Heft und erkläre dein Vorgehen.