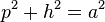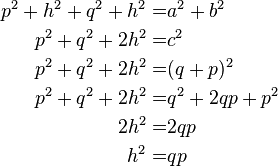Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Höhensatz: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
< WDG | Klasse 9 | Pythagoras
(Die Seite wurde neu angelegt: „<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:50%; align:center; "> <span styl…“) |
|||
| Zeile 4: | Zeile 4: | ||
* Notiere dir, anhand der [[WDG/Klasse_9/Pythagoras/Flipped_Classroom|vorgegebenen Fragen]], Bemerkungen in OneNote. | * Notiere dir, anhand der [[WDG/Klasse_9/Pythagoras/Flipped_Classroom|vorgegebenen Fragen]], Bemerkungen in OneNote. | ||
* '''Luca, Michael, Alexander, David''' erstellen einen [[WDG/Klasse_9/Pythagoras/Flipped_Classroom|Hefteintrag in Word]]. | * '''Luca, Michael, Alexander, David''' erstellen einen [[WDG/Klasse_9/Pythagoras/Flipped_Classroom|Hefteintrag in Word]]. | ||
| − | * Für Interessierte gibt es auch noch die Herleitung | + | * Für Interessierte gibt es auch noch die Herleitung des Höhensatzes (Diese Aufgabe ist optional). |
</div> | </div> | ||
Version vom 26. Oktober 2018, 19:15 Uhr
Arbeitsaufträge:
- Schaue dir das Video zum Höhensatz genau an.
- Notiere dir, anhand der vorgegebenen Fragen, Bemerkungen in OneNote.
- Luca, Michael, Alexander, David erstellen einen Hefteintrag in Word.
- Für Interessierte gibt es auch noch die Herleitung des Höhensatzes (Diese Aufgabe ist optional).
Inhaltsverzeichnis[Verbergen] |
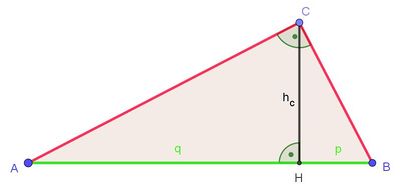
Der Höhensatz des Euklid
Merke: Höhensatz
Wenn ein Dreieck 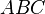 bei
bei 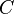 rechtwinklig ist, dann gilt folgender Zusammenhang:
rechtwinklig ist, dann gilt folgender Zusammenhang: 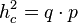 , wobei die Höhe die Seite
, wobei die Höhe die Seite  in
in 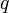 und
und 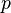 teilt.
teilt.
Für Interessierte: Beweis des Höhensatzes (Optional)
Hefteintrag
Quellenangabe
Video "Höhensatz des Euklid" von Lehrerschmidt, über https://www.youtube.com/watch?v=-fKlC5J_xLY (Zugriff am 20.10.2018)
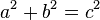 und
und 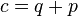 .
.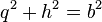 und
und