Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Test: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 11: | Zeile 11: | ||
<popup name="Lösung 1: Ableitung von f(x)">Die Ableitung von <math>f(x)</math> ist <math>f'(x)=-2/3x</math>.</popup> | <popup name="Lösung 1: Ableitung von f(x)">Die Ableitung von <math>f(x)</math> ist <math>f'(x)=-2/3x</math>.</popup> | ||
<popup name="Lösung 2: Steigung im Punkt x=-3">Die Steigung im Punkt <math>x=-3</math> ist <math>f'(x)=-2/3x=2</math>.</popup> | <popup name="Lösung 2: Steigung im Punkt x=-3">Die Steigung im Punkt <math>x=-3</math> ist <math>f'(x)=-2/3x=2</math>.</popup> | ||
| − | <popup name=" | + | <popup name="Lösung 3: y-Achsenabschnitt">Der y-Achsenabschnitt ist <math>0=2*(-3)+b</math>, also <math>b=6</math>.</popup> |
<popup name="Lösung 4: Tangentengleichung">Die Gleichung der Tangente lautet <math>y=2x+6</math>.</popup> | <popup name="Lösung 4: Tangentengleichung">Die Gleichung der Tangente lautet <math>y=2x+6</math>.</popup> | ||
}} | }} | ||
Version vom 13. November 2018, 18:23 Uhr
|
Die Tangente an die Funktion |
|
Bestimme die Gleichung der Tangente an die Funktion
|
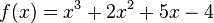 im Punkt
im Punkt 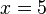 soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
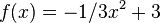 im Punkt
im Punkt 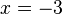 .
.
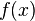 ist
ist 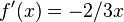 .
.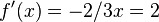 .
.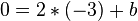 , also
, also 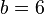 .
.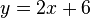 .
.
