Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Test: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
(→Aufgabenteil b)) |
|||
| (13 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
| − | = | + | {{Aufgaben|3|Die Tangente an die Funktion <math>f(x)=x^3+2x^2+5x-4</math> im Punkt <math>x=5</math> soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen. |
| − | === | + | <iframe src="https://learningapps.org/watch?v=ppge2zo5318" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| − | Bestimme die Gleichung der Tangente an die Funktion f(x)=-1/3x | + | <popup name="Tipp">Eine Tangentengleichung hat die Form <math>y=mx+b</math>, wobei <math>m</math> die Steigung der Tangente ist und <math>b</math> der y-Achsenabschnitt.</popup> |
| − | <popup name="Tipp | + | }} |
| − | < | + | {{Aufgaben| 4| |
| + | Bestimme die Gleichung der Tangente an die Funktion <math>f(x)=-1/3x^2+3</math> im Punkt <math>x=-3</math>. | ||
| + | <popup name="Tipp">Erinnere dich zuerst daran, wie eine Tangentengleichung aussieht. Aufgabe 3 kann dir dabei helfen. | ||
| + | Um die Steigung m zu ermitteln, benötigst du die Ableitung und musst anschließend die Ableitung im Punkt <math>x=-3</math> bestimmen. Was ist also der Zusammenhang zwischen der Ableitung in dem Punkt und der Steigung? | ||
| + | Wenn du die Steigung berechnet hast, fehlt dir nur noch der y-Achsenabschnitt. Dazu setzt du alle bekannten Werte in die allgemeine Tangentengleichung ein und formst um. | ||
| − | + | Schließlich kannst du die vollständige Tangentengleichung aufstellen. </popup> | |
| − | + | <popup name="Lösung 1: Ableitung von f(x)">Die Ableitung von <math>f(x)</math> ist <math>f'(x)=-2/3x</math>.</popup> | |
| − | <popup name=" | + | <popup name="Lösung 2: Steigung im Punkt x=-3">Die Steigung im Punkt <math>x=-3</math> ist <math>f'(x)=-2/3x=2</math>.</popup> |
| − | <popup name="Lösung | + | <popup name="Lösung 3: y-Achsenabschnitt">Der y-Achsenabschnitt ist <math>0=2*(-3)+b</math>, also <math>b=6</math>.</popup> |
| − | <popup name="Lösung | + | <popup name="Lösung 4: Tangentengleichung">Die Gleichung der Tangente lautet <math>y=2x+6</math>.</popup> |
| + | |||
| + | }} | ||
Aktuelle Version vom 8. Dezember 2018, 13:01 Uhr
|
Die Tangente an die Funktion |
|
Bestimme die Gleichung der Tangente an die Funktion
|
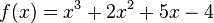 im Punkt
im Punkt 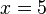 soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
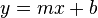 , wobei
, wobei 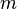 die Steigung der Tangente ist und
die Steigung der Tangente ist und 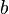 der y-Achsenabschnitt.
der y-Achsenabschnitt.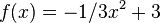 im Punkt
im Punkt 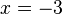 .
.
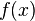 ist
ist 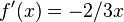 .
.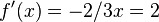 .
.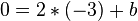 , also
, also 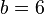 .
.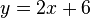 .
.
