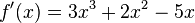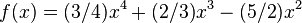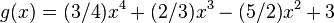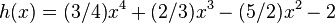Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Graphisches Ableiten: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
(→‎Forderaufgaben)
 
(19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 8: Zeile 8:
  
 
</td></tr></table></center> </div>  
 
</td></tr></table></center> </div>  
 +
 +
  
 
__TOC__
 
__TOC__
Zeile 16: Zeile 18:
  
  
−
<iframe src="https://learningapps.org/watch?app=1688183" style="border:0px;width:100%;height:800px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
<iframe src="https://learningapps.org/watch?app=1688183" style="border:0px;width:100%;height:600px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
  
 
<popup name="Tipp 1">In welchen Intervallen steigen oder fallen die Graphen von f(x)? Wie sieht hier die Ableitung aus?</popup>
 
<popup name="Tipp 1">In welchen Intervallen steigen oder fallen die Graphen von f(x)? Wie sieht hier die Ableitung aus?</popup>
Zeile 27: Zeile 29:
 
{{Aufgaben|2 Wie sieht der Ableitungsgraph aus?|Die Abbildung zeigt den Graphen einer Funktion f(x). Welche Annahmen kannst du über f'(x) treffen? Vervollständige die Sätze.
 
{{Aufgaben|2 Wie sieht der Ableitungsgraph aus?|Die Abbildung zeigt den Graphen einer Funktion f(x). Welche Annahmen kannst du über f'(x) treffen? Vervollständige die Sätze.
  
−
[[Datei:Aufgabe 3.png|f(x)=5x^(4)+3x^(3)-4x^(2)|1000px|links|rahmenlos]]<br />
+
[[Datei:Aufgabe 3.png|f(x)=5x^(4)+3x^(3)-4x^(2)|800px|links|rahmenlos]]<br />
  
  
Zeile 59: Zeile 61:
  
  
−
 
+
<iframe src="https://learningapps.org/watch?v=pfcxan3w218" style="border:0px;width:70%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
−
<iframe src="https://learningapps.org/watch?v=pfcxan3w218" style="border:0px;width:80%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
 
<popup name="Tipp 'Grad bestimmen'">Den Grad einer Funktion kann man am höchsten Exponenten ablesen. Er gibt die maximale Anzahl an Nullstellen an.</popup> }}
 
<popup name="Tipp 'Grad bestimmen'">Den Grad einer Funktion kann man am höchsten Exponenten ablesen. Er gibt die maximale Anzahl an Nullstellen an.</popup> }}
  
Zeile 78: Zeile 79:
  
 
{{Aufgaben|4 Wie sieht der Graph von f(x) aus?|
 
{{Aufgaben|4 Wie sieht der Graph von f(x) aus?|
−
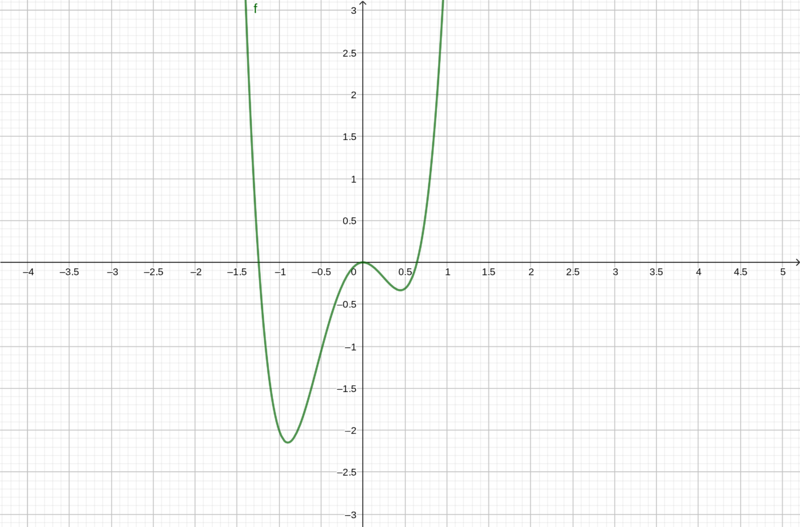
'''a)''' Die Abbildung zeigt den Graphen einer Ableitungsfunktion f(x). Skizziere die dazugehörige Funktion F(x) in deinem Heft und erkläre dein Vorgehen.
+
'''a)''' Die Abbildung zeigt den Graphen einer Ableitungsfunktion f'(x). Skizziere die dazugehörige Funktion f(x) in deinem Heft und erkläre dein Vorgehen.
  
−
[[Datei:Aufgabe 4.png|f(x)=3x^(3)+2x^(2)-5x|600px|links|rahmenlos]]<br />
+
[[Datei:Aufgabe 4n.png|f(x)=3x^(3)+2x^(2)-5x|600px|links|rahmenlos]]<br />
  
  
Zeile 117: Zeile 118:
 
<popup name="Tipp 2">Was bedeuten negative beziehungsweise positive Funktionswerte der Ableitungsfunktion für ihre Stammfunktion?</popup>
 
<popup name="Tipp 2">Was bedeuten negative beziehungsweise positive Funktionswerte der Ableitungsfunktion für ihre Stammfunktion?</popup>
 
<popup name="Tipp 3">Liegt eine Nullstelle in der Ableitung vor, hat die Stammfunktion hier eine Extremstelle. Verläuft die Ableitungsfunktion unterhalb der x-Achse, so fällt die Stammfunktion auf diesem Intervall. Für einen Verlauf oberhalb der x-Achse steigt die Stammfunktion.</popup>
 
<popup name="Tipp 3">Liegt eine Nullstelle in der Ableitung vor, hat die Stammfunktion hier eine Extremstelle. Verläuft die Ableitungsfunktion unterhalb der x-Achse, so fällt die Stammfunktion auf diesem Intervall. Für einen Verlauf oberhalb der x-Achse steigt die Stammfunktion.</popup>
−
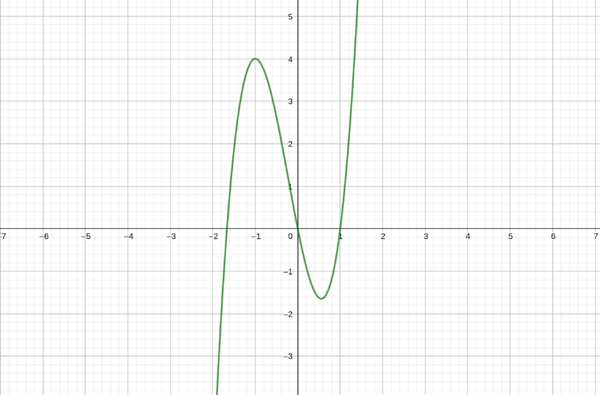
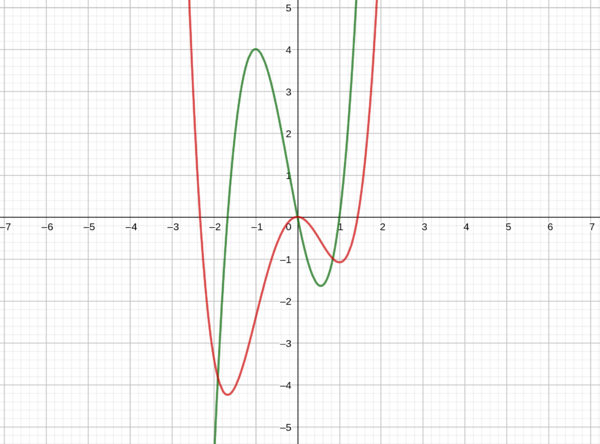
<popup name="Lösung">Der rote Graph ist der Graph von F(x). Wenn f(x) negativ ist, fällt F(x). Ist f(x) positiv, so steigt F(x). An den Nullstellen von f(x) sind die Extrema von F(x).
+
<popup name="Lösung">Der rote Graph ist der Graph von f(x). Wenn f'(x) negativ ist, fällt f(x). Ist f'(x) positiv, so steigt f(x). An den Nullstellen von f'(x) sind die Extrema von f(x).
  
  
 +
[[Datei:Lösung 4n.png|f(x)=3x^(3)+2x^(2)-5xF(x)=(3/4)x^(4)+(2/3)x^(3)-(5/2)x^(2)|600px|links|rahmenlos]]<br />
 +
</popup>
  
  
−
[[Datei:Lösung 4.png|f(x)=3x^(3)+2x^(2)-5xF(x)=(3/4)x^(4)+(2/3)x^(3)-(5/2)x^(2)|600px|links|rahmenlos]]<br />
+
'''b)''' Gibt es nur eine Möglichkeit, wie der Funktionsgraph verlaufen kann? Wie verändert eine Konstante den Verlauf von F(x) und was passiert mit ihr, wenn man F(x) ableitet?
−
</popup>
+
 
 +
<popup name="Lösung">
 +
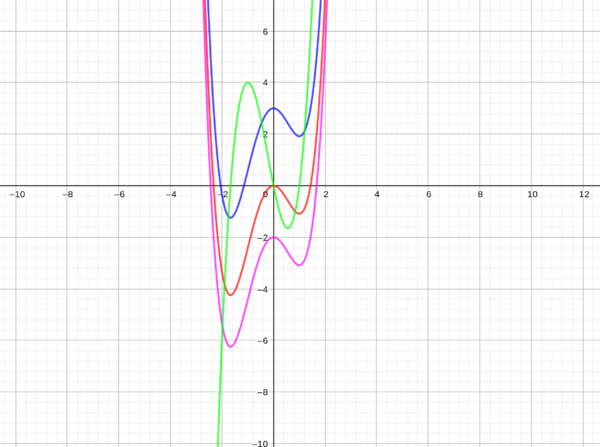
Im Bild siehst du den Graph der Ableitungsfunktion f' in grün. Die einfachst Möglichkeit einer Stammfunktion ist die Funktion f deren Graph hier in rot abgebildet ist. Die Funktion g erhält man durch das addieren der Konstante 3, der Graph ist hier in blau dargestellt. Bei der Funktion h wurde die Konstante 2 abgezogen, sie ist hier in lila dargestellt.
 +
 
 +
<math>f'(x)=3x^3+2x^2-5x</math>
 +
 
 +
<math>f(x)=(3/4)x^4+(2/3)x^3-(5/2)x^2</math>
 +
 
 +
<math>g(x)=(3/4)x^4+(2/3)x^3-(5/2)x^2+3</math>
 +
 
 +
<math>h(x)=(3/4)x^4+(2/3)x^3-(5/2)x^2-2</math>
 +
 
 +
 
 +
 
 +
 
 +
 
 +
[[Datei:Lösung 4b.png|f(x)=3x^(3)+2x^(2)-5xF(x)=(3/4)x^(4)+(2/3)x^(3)-(5/2)x^(2)|600px|links|rahmenlos]]<br />
 +
</popup>}}
  
  
−
'''b)''' Gibt es nur eine Möglichkeit, wie der Funktionsgraph verlaufen kann? Wie verändert eine Konstante den Verlauf von F(x) und was passiert mit ihr, wenn man F(x) ableitet? }}
 
  
−
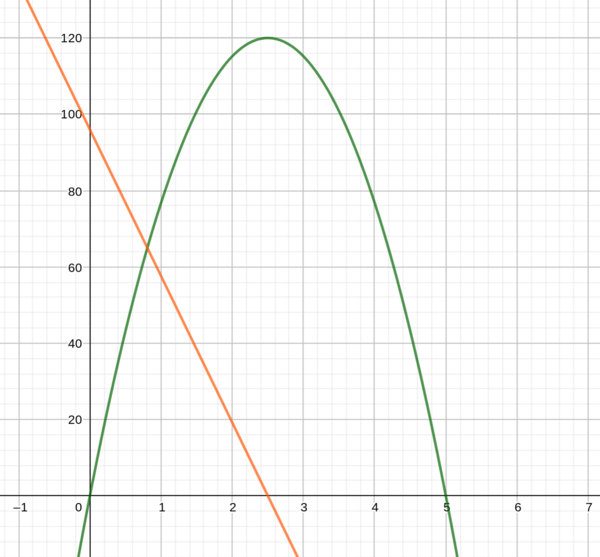
{{Aufgaben|5 Zugfahrt|Auf der Fahrt zwischen Münster und Münster Hiltrup erreichen die Züge einmal die Geschwindigkeit von 120Km/h. Die Funktion f(x) beschreibt die Geschwindigkeit des Zuges auf dieser Strecke, dabei stehen die x-Werte für die gefahrene Zeit in Minuten und die Funktionswerte f(x) für die gefahrene Geschwindigkeit. Die Funktionswerte findest du in der Tabelle unten.  
+
{{Aufgaben|5 Zugfahrt|Auf der Fahrt zwischen Münster und Münster Hiltrup erreichen die Züge einmal die Geschwindigkeit von 120km/h. Die Funktion f(x) beschreibt die Geschwindigkeit des Zuges auf dieser Strecke, dabei stehen die x-Werte für die gefahrene Zeit in Minuten und die Funktionswerte f(x) für die gefahrene Geschwindigkeit. Die Funktionswerte findest du in der Tabelle unten.  
  
 
'''a)''' Skizziere die Funktion und ihre Ableitung in dein Heft.
 
'''a)''' Skizziere die Funktion und ihre Ableitung in dein Heft.
Zeile 150: Zeile 169:
 
|}
 
|}
  
−
<popup name="Lösung zu a)">[[Datei:Lösung 5.png|f(x)=-19,2x^(2)+96xf'(x)=-38,4x+96|600px|links|rahmenlos]]</popup>
+
<popup name="Lösung zu a)">Die Funktion kannst du anhand der Werte aus der Tabelle zeichnen. Die Ableitung ist hier in rot zu sehen.
 +
 
 +
 
 +
[[Datei:Lösung 5n.png|f(x)=-19,2x^(2)+96xf'(x)=-38,4x+96|600px|links|rahmenlos]]</popup>
  
 
<popup name="Lösung zu b)">Die Funktion hat Grad 2, da sie ein Extremum besitzt.</popup>
 
<popup name="Lösung zu b)">Die Funktion hat Grad 2, da sie ein Extremum besitzt.</popup>
Zeile 157: Zeile 179:
  
 
<popup name="Lösung zu d)">Die Geschwindigkeit ändert sich am stärksten in der ersten sowie der letzten Minute der Fahrt. In der ersten Minute beschleunigt der Zug am stärksten, in der letzten Minute bremst er am stärksten ab.</popup>
 
<popup name="Lösung zu d)">Die Geschwindigkeit ändert sich am stärksten in der ersten sowie der letzten Minute der Fahrt. In der ersten Minute beschleunigt der Zug am stärksten, in der letzten Minute bremst er am stärksten ab.</popup>
 +
 +
[[Kategorie:Digitale Werkzeuge in der Schule|!]]

Aktuelle Version vom 28. Dezember 2018, 00:01 Uhr

In diesem Lernpfad kannst du üben, Funktionen und ihre Ableitungen anhand ihrer Graphen zu untersuchen. Der Zusammenhang zwischen besonderen Punkten und Merkmalen einer Funktion und ihrer Ableitung stehen hier im Vordergrund. Im Folgenden findest du Aufgaben, um deine Kenntnisse im graphischen Ableiten zu vertiefen (Forderaufgaben) aber auch, um Lücken zu schließen und Stoff zu wiederholen (Förderaufgaben). Unter jeder Aufgabe gibt es Hilfestellungen, auf die du zurückgreifen kannst, wenn du mal nicht weiterkommst.


  • Wenn dir das Thema noch Schwierigkeiten bereitet, beginne mit den Förderaufgaben (Aufgabe 1 bis Aufgabe 3).
  • Wenn du dich bereits sicher fühlst, probiere die Forderaufgaben (Aufgabe 3 bis Aufgabe 5).


Inhaltsverzeichnis


Förderaufgaben

Stift.gif   Aufgabe 1 Graphen zuordnen

Ordne den Graphen der Funktionen f(x) den richtigen Ableitungsgraphen zu, indem du jeweils zwei Kästchen per Mausklick zusammenführst. Das erreichst du, indem du die linke Maustaste über einem Kästchen gedrückt hältst und das Kästchen anschließend bewegst. Klicke anschließend auf den blauen Punkt in der rechten unteren Ecke der Aufgabe, um deine Lösungen zu kontrollieren.



Stift.gif   Aufgabe 2 Wie sieht der Ableitungsgraph aus?

Die Abbildung zeigt den Graphen einer Funktion f(x). Welche Annahmen kannst du über f'(x) treffen? Vervollständige die Sätze.

f(x)=5x^(4)+3x^(3)-4x^(2)
















Bereit für die Forderaufgaben? Teste dein Wissen!

Stift.gif   Aufgabe 3 Wer wird Millionär?

Finde die richtige Antwort. Du kannst die App mit einem Klick auf das Zeichen oben rechts im Vollbildmodus anzeigen lassen.

Forderaufgaben

Stift.gif   Aufgabe 4 Wie sieht der Graph von f(x) aus?

a) Die Abbildung zeigt den Graphen einer Ableitungsfunktion f'(x). Skizziere die dazugehörige Funktion f(x) in deinem Heft und erkläre dein Vorgehen.

f(x)=3x^(3)+2x^(2)-5x


















b) Gibt es nur eine Möglichkeit, wie der Funktionsgraph verlaufen kann? Wie verändert eine Konstante den Verlauf von F(x) und was passiert mit ihr, wenn man F(x) ableitet?


Stift.gif   Aufgabe 5 Zugfahrt

Auf der Fahrt zwischen Münster und Münster Hiltrup erreichen die Züge einmal die Geschwindigkeit von 120km/h. Die Funktion f(x) beschreibt die Geschwindigkeit des Zuges auf dieser Strecke, dabei stehen die x-Werte für die gefahrene Zeit in Minuten und die Funktionswerte f(x) für die gefahrene Geschwindigkeit. Die Funktionswerte findest du in der Tabelle unten.

a) Skizziere die Funktion und ihre Ableitung in dein Heft.

b) Die Daten sollen durch ein Programm verarbeitet werden. Dazu wird eine Funktionsgleichung benötigt. Welchen Grad muss diese Funktion haben?

c) Welchen Grad hat die Ableitung?

d) Wann ändert sich die Geschwindigkeit am stärksten? Begründe mit Hilfe der Ableitung.

x 0 1 2 3 4 5
f(x) 0 76,8 115,2 115,2 76,8 0
Von „https://projektwiki.zum.de/index.php?title=Digitale_Werkzeuge_in_der_Schule/Trainingsfeld_Ableitungen/Graphisches_Ableiten&oldid=61814“