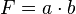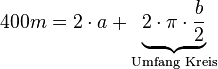Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).KW 3: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Wochenplan KW 3 === <div style="margin:0px; margin-right:50px; border:thick double red; padding: 1em 1em 1em 1em; background-color:white; width:40%; alig…“) |
|||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
</div> | </div> | ||
<br /> | <br /> | ||
| + | |||
| + | ====<span style="color:green">Aufgabe I</span>==== | ||
| + | Wandle in alle drei Darstellungsformen für quadratische Funktionsterme um. | ||
| + | #) <math>f(x)=-3x^2-3x+18</math> | ||
| + | #) <math>g(x)=-(x+4)^2-1</math> | ||
| + | #) <math>h(x)=4(x-5)(x-2)</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | ====<span style="color:green">Aufgabe II</span>==== | ||
| + | Bauer Max besitzt einen Acker mit 60m Länge und 40m Breite. Auf seinem Feld soll jedoch Baugrund entstehen und die Gemeinde macht ihm zur Entschädigung folgendes Angebot:<br /> | ||
| + | Damit die Fläche ''größer'' wirkt, soll die Breite um x m vergrößert werden und dafür die Länge um x m verkleinert werden. <br /> | ||
| + | <br /> | ||
| + | Er überlegt, ob er das Angebot annehmen soll, oder ob er die gleichen Längenmaße wieder nimmt. <br /> | ||
| + | # Bestimme für welchen Wert von x der Acker den größten Flächeninhalt hat. | ||
| + | # Welchen Flächeninhalt hat Bauer Max's Feld dann? | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ====<span style="color:green">Aufgabe III</span>==== | ||
| + | Der Sportplatz am Gymnasium Pocking wird neu angelegt. Es ist geplant einen Fußballplatz mit einer darum führenden 400m Bahn zu bauen. <br /> | ||
| + | Die Seitenlängen des Fußballplatzes werden mit a und b bezeichnet.<br /> | ||
| + | <br /> | ||
| + | * Bestimme a und b so, dass der Flächeninhalt des rechteckigen Fußballplatzes maximal wird. | ||
| + | <br /> | ||
| + | [[Datei:Laufbahn.JPG|400px]] | ||
| + | <br /> | ||
| + | Tipp 1: {{versteckt|Überlege dir, wie sich Haupt- und Nebenbedingungen zusammensetzen. <br /> | ||
| + | Hauptbedingung: rechteckige Fläche des Fußballfelds <br /> | ||
| + | Nebenbedingung: Laufbahn (2 Geraden der Länge a + und 2 Halbkreise mit Radius <math>\frac{b}{2}</math>) }} | ||
| + | <br /> | ||
| + | Tipp 2: {{versteckt|Hauptbedingung: <math>F=a \cdot b</math> <br /> | ||
| + | Nebenbedingung: <math>400m = 2 \cdot a + \underbrace{2 \cdot \pi \cdot \frac{b}{2}}_{\text{Umfang Kreis}} </math> }} | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ---- | ||
| + | <br /> | ||
| + | ====Lösungen der Aufgaben aus KW 3:<br />==== | ||
| + | [[Datei:Verbesserung KW 3.pdf|thumb|left|Verbesserung Hausaufgabe KW 3]] | ||
Aktuelle Version vom 22. Januar 2019, 15:24 Uhr
Inhaltsverzeichnis |
Wochenplan KW 3
Besprechung Mi 23.01.
- grüne Aufgaben sind Pflichtaufgaben
- orange Aufgaben sind optional zur vertiefenden Übung
Aufgabe I
Wandle in alle drei Darstellungsformen für quadratische Funktionsterme um.
- )
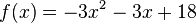
- )
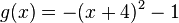
- )
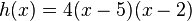
Aufgabe II
Bauer Max besitzt einen Acker mit 60m Länge und 40m Breite. Auf seinem Feld soll jedoch Baugrund entstehen und die Gemeinde macht ihm zur Entschädigung folgendes Angebot:
Damit die Fläche größer wirkt, soll die Breite um x m vergrößert werden und dafür die Länge um x m verkleinert werden.
Er überlegt, ob er das Angebot annehmen soll, oder ob er die gleichen Längenmaße wieder nimmt.
- Bestimme für welchen Wert von x der Acker den größten Flächeninhalt hat.
- Welchen Flächeninhalt hat Bauer Max's Feld dann?
Aufgabe III
Der Sportplatz am Gymnasium Pocking wird neu angelegt. Es ist geplant einen Fußballplatz mit einer darum führenden 400m Bahn zu bauen.
Die Seitenlängen des Fußballplatzes werden mit a und b bezeichnet.
- Bestimme a und b so, dass der Flächeninhalt des rechteckigen Fußballplatzes maximal wird.
Überlege dir, wie sich Haupt- und Nebenbedingungen zusammensetzen.
Hauptbedingung: rechteckige Fläche des Fußballfelds
 )
)
Tipp 2:
Hauptbedingung: