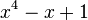Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Verhalten nahe 0: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
(Die Seite wurde neu angelegt: „{{Aufgaben|1|Gegeben ist die Funktion f mit <math>f(x)=1/6 x^4-4/3x^2-3/2</math>. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0…“) |
|||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{Aufgaben|1| | + | {{Aufgaben|1 Zuordnung von Graph und Funktionsgleichung|<iframe src="https://learningapps.org/watch?v=p391nnp6k19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| − | {{Aufgaben|2|Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0. | + | <popup Name="Tipp">Durch Klicken auf den Graphen wird dieser größer und ist besser zu erkennen.</popup> |
| + | <popup Name="Tipp">Bsp. Schreibweise: Die Funktion <math>f(x)=x^4+x-1</math> hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie <math>g(x)=x^4</math>. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich. | ||
| + | Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie <math>h(x)=x-1</math>. Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat.</popup> | ||
| + | }} | ||
| + | |||
| + | {{Aufgaben|2 Wahr oder falsch?!|<iframe src="https://learningapps.org/watch?v=p8psqbyhc19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | }} | ||
| + | |||
| + | |||
| + | {{Aufgaben|3|Gegeben ist die Funktion f mit <math>f(x)=1/6 x^4-4/3x^2-3/2</math>. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.}} | ||
| + | |||
| + | {{Aufgaben|4|Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0. | ||
'''a)''' | '''a)''' | ||
| Zeile 10: | Zeile 21: | ||
'''c)''' | '''c)''' | ||
| − | <math>h(x)= | + | <math>h(x)=\sqrt{\;x^2}-1</math> |
<popup Name="Tipp">Es macht Sinn, die Klammern erst auszumultiplizieren.</popup> | <popup Name="Tipp">Es macht Sinn, die Klammern erst auszumultiplizieren.</popup> | ||
| − | <popup Name="Lösung">a) x gegen Unendlich wie <math>x^2</math>, also | + | <popup Name="Lösung">a) x gegen Unendlich wie <math>x^2</math>, also x--> -∞ = ∞ </popup> |
| + | }} | ||
| + | |||
| + | {{Aufgaben|5|Skizziere folgende Graphen. Achte dabei auf das Verhalten nahe Null und gegen Unendlich. | ||
| + | |||
| + | '''a)''' | ||
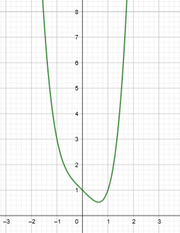
| + | <math>x^4-x+1</math> | ||
| + | |||
| + | '''b)''' | ||
| + | |||
| + | '''c)''' | ||
| + | |||
| + | <popup Name="Lösung">a) [[Datei:Geogebra7.png|miniatur|links]]</popup> | ||
}} | }} | ||
Aktuelle Version vom 12. November 2019, 14:54 Uhr
|
|
|
|
|
Gegeben ist die Funktion f mit |
|
Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0. a)
b)
c)
|
|
Skizziere folgende Graphen. Achte dabei auf das Verhalten nahe Null und gegen Unendlich. a)
b) c) |
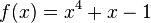 hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie
hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie 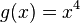 . Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie
. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
Die Funktion verhält sich nahe 0 wie der x-Wert mit dem kleinsten Exponenten und dem absoluten Glied, also wie 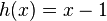 . Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat.
. Damit ist es nahe 0 annähernd eine Gerade, die die Steigung 1 und den y-Achsenabschnitt -1 hat.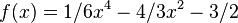 . Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
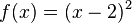
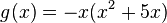
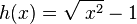
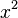 , also x--> -∞ = ∞
, also x--> -∞ = ∞