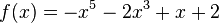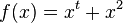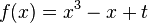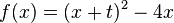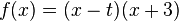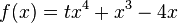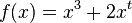Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Symmetrie von ganzrationalen Funktionen: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{Aufgaben|1| | + | {{Aufgaben|1 Wahr oder falsch?|<iframe src="https://learningapps.org/watch?v=pv4yx7vst19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| + | <popup Name="Lösung">Der Graph einer Funktion f mit der Definitionsmenge <math>D<sub>f</sub></math> ist genau dann achsensymmetrisch zur y-Achse, wenn für alle x im Definitionsbereich: <math>f(-x)=f(x)</math> gilt. | ||
| + | Der Graph einer Funktion f mit der Definitionsmenge <math>D<sub>f</sub></math> ist genau dann punktsymmetrisch zum Ursprung, wenn für alle x im Definitionsbereich: '''<math>f(-x)=-f(x)</math>''' gilt. | ||
| + | Der Graph einer Funktion f verläuft genau dann achsensymmetrisch zur y-Achse, wenn der Funktionsterm nur '''gerade''' Exponenten enthält. | ||
| + | Der Graph einer Funktion f verläuft genau dann punktsymmetrisch zum Ursprung, wenn der Funktionsterm nur ungerade Exponenten enthält. | ||
| + | Man bezeichnet eine Funktion als gerade Funktion, wenn ihr Graph achsensymmetrisch zur y-Achse verläuft.</popup> | ||
| + | }} | ||
| + | |||
| + | {{Aufgaben|2| | ||
'''a)''' | '''a)''' | ||
<iframe src="https://learningapps.org/watch?v=p5njp3xva19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=p5njp3xva19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
<popup Name="Tipp"> Multipliziert die Gleichungen erst aus, bevor ihr entscheidet.</popup> | <popup Name="Tipp"> Multipliziert die Gleichungen erst aus, bevor ihr entscheidet.</popup> | ||
| − | <popup Name="Tipp"> Eine Funktion ist achsensymmetrisch | + | <popup Name="Tipp"> Eine Funktion ist achsensymmetrisch zur y-Achse, wenn die Gleichung nur '''gerade Exponenten''' und das absolute Glied (<math>a\cdot x^0</math>) enthält. |
Eine Funktion ist punktsymmetrisch zum Ursprung, wenn die Gleichung nur '''ungerade Exponenten''' enthält.</popup> | Eine Funktion ist punktsymmetrisch zum Ursprung, wenn die Gleichung nur '''ungerade Exponenten''' enthält.</popup> | ||
| + | <popup Name="Tipp">Eine Funktion ist achsensymmetrisch zur y-Achse, wenn für alle x gilt: <math>f(-x)=f(x)</math>. | ||
| + | Eine Funktion ist punktsymmetrisch zum Ursprung, wenn für alle x gilt: <math>f(-x)=-f(x)</math></popup> | ||
<popup Name="Lösung"> Punktsymmetrie: <math>f(x)=x^3</math>,<math>f(x)=-x^3</math>,<math>f(x)=x^5</math>,<math>f(x)=x^5+x^3+x</math>,<math>f(x)=(x-3)*x*(x+3)</math>,<math>f(x)=(x^2-9)*x</math> | <popup Name="Lösung"> Punktsymmetrie: <math>f(x)=x^3</math>,<math>f(x)=-x^3</math>,<math>f(x)=x^5</math>,<math>f(x)=x^5+x^3+x</math>,<math>f(x)=(x-3)*x*(x+3)</math>,<math>f(x)=(x^2-9)*x</math> | ||
| Zeile 14: | Zeile 24: | ||
'''b)''' Greift euch drei Beispiele heraus und schreibt eine ausführliche Begründung für eure Einordnung. | '''b)''' Greift euch drei Beispiele heraus und schreibt eine ausführliche Begründung für eure Einordnung. | ||
<popup Name="Lösung">Bsp.: <math>f(x)=x^5+x^3+x</math>, die Gleichung hat die Exponenten 5,3,1. Diese sind allesamt ungerade, also ist die Funktion punktsymmetrisch zum Ursprung.</popup> | <popup Name="Lösung">Bsp.: <math>f(x)=x^5+x^3+x</math>, die Gleichung hat die Exponenten 5,3,1. Diese sind allesamt ungerade, also ist die Funktion punktsymmetrisch zum Ursprung.</popup> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| Zeile 38: | Zeile 40: | ||
'''f)'''<math>f(x)=x^3+2x^t</math> | '''f)'''<math>f(x)=x^3+2x^t</math> | ||
| − | <popup Name=" | + | <popup Name="Tipp">'''a),f)'''Es gibt mehr als eine Lösung. |
'''c)'''Klammer ausmultiplizieren. | '''c)'''Klammer ausmultiplizieren. | ||
'''d)'''Beachte die dritte binomische Formel.</popup> | '''d)'''Beachte die dritte binomische Formel.</popup> | ||
| Zeile 51: | Zeile 53: | ||
'''e)'''Für kein t --> keine Symmetrie | '''e)'''Für kein t --> keine Symmetrie | ||
| − | '''f)'''Für alle ungeraden t, also …-3,-1,1,3,5,... | + | '''f)'''Für alle ungeraden t, also …-3,-1,1,3,5,... --> Punktsymmetrie |
</popup> | </popup> | ||
}} | }} | ||
Aktuelle Version vom 13. November 2019, 17:54 Uhr
|
|
|
a) b) Greift euch drei Beispiele heraus und schreibt eine ausführliche Begründung für eure Einordnung. |
|
Für welche t ist der Graph der Funktion f symmetrisch zum Ursprung oder zur y-Achse? a) b) c) d) e) f) |
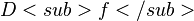 ist genau dann achsensymmetrisch zur y-Achse, wenn für alle x im Definitionsbereich:
ist genau dann achsensymmetrisch zur y-Achse, wenn für alle x im Definitionsbereich: 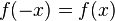 gilt.
gilt.
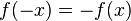 gilt.
Der Graph einer Funktion f verläuft genau dann achsensymmetrisch zur y-Achse, wenn der Funktionsterm nur gerade Exponenten enthält.
Der Graph einer Funktion f verläuft genau dann punktsymmetrisch zum Ursprung, wenn der Funktionsterm nur ungerade Exponenten enthält.
gilt.
Der Graph einer Funktion f verläuft genau dann achsensymmetrisch zur y-Achse, wenn der Funktionsterm nur gerade Exponenten enthält.
Der Graph einer Funktion f verläuft genau dann punktsymmetrisch zum Ursprung, wenn der Funktionsterm nur ungerade Exponenten enthält.
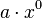 ) enthält.
Eine Funktion ist punktsymmetrisch zum Ursprung, wenn die Gleichung nur ungerade Exponenten enthält.
) enthält.
Eine Funktion ist punktsymmetrisch zum Ursprung, wenn die Gleichung nur ungerade Exponenten enthält.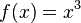 ,
,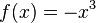 ,
,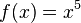 ,
,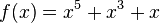 ,
,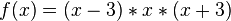 ,
,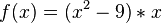
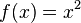 ,
,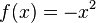 ,
,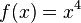 ,
,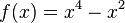 ,
,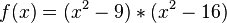
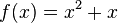 ,
,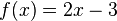 ,
,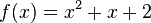 ,
,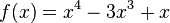 ,
,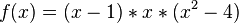 ,
,