Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Multiplikation und Division von Brüchen: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
 
(13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
<span style="color: blue">'''Multiplikation von Brüchen:'''</span>  
+
<div style="margin:0; margin-right:4px; margin-left:4px; border:5px solid #C00000; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;">
 +
 
 
<br />
 
<br />
 +
Das Rechnen mit Brüchen fällt vielen von uns schwer, weshalb ich im Folgenden das Berechnen von Brüchen bei einer Multiplikation, sowie Division erklären und erleichtern möchte.
 
<br />
 
<br />
−
<span style="color: red">'''<u>Aber bevor du los legst, habe ich hier noch einmal kurz erklärt, wie man richtig Brüche miteinander multipliziert:</u></span>
+
<br />
 +
<span style="color: blue">'''Multiplikation von Brüchen:'''</span>
 +
<br />
 +
 
 +
<span style="color: red">'''<u>Um euch effektiver helfen zu können, habe ich in diesem Video kurz erklärt, wie man richtig Brüche miteinander multipliziert→</u></span>
 
'''
 
'''
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
Zeile 13: Zeile 19:
  
 
</div>
 
</div>
 +
<br />
 +
<br />
 +
<span style="color: blue">'''Division von Brüchen:'''</span>
 +
<br />
 +
<br />
 +
Hierbei spielt der Kehrwert eine große Rolle. '''Kehrwert''' heißt, dass der '''Zweite Bruch umgedreht''' wird, also→ '''Zähler und Nenner''' werden '''vertauscht'''. Nach der Umwandlung, '''ändert sich''' auch das '''Rechenzeichen''', und das '''"÷"''' wird zu einem '''"·"'''. Nun werden die '''2 Brüche miteinander multipliziert''' und tadaaa, du hast die Lösung. Am Ende kannst du nochmal überprüfen, ob du das Ergebnis '''kürzen''' kannst. So schwer war das doch gar nicht oder?:)
 +
<br />
 +
<br />
 +
Aber falls du es noch nicht ganz verstanden hast, habe ich hier ein Beispiel für dich:
 +
<br />
 +
&nbsp;&nbsp;<math>\frac{2}{4}</math>&nbsp;&nbsp; : &nbsp;&nbsp;<math>\frac{5}{2}</math>&nbsp;&nbsp; = &nbsp;&nbsp;<math>\frac{2}{4}</math>&nbsp;&nbsp;<span style="color: red">'''·'''</span>&nbsp;&nbsp;<math>\frac{2}{5}</math>&nbsp;&nbsp; = &nbsp;&nbsp;<math>\frac{4}{20}</math>&nbsp;&nbsp; = &nbsp;&nbsp;<math>\frac{1}{5}</math>&nbsp;&nbsp;

Aktuelle Version vom 23. November 2017, 14:13 Uhr


Das Rechnen mit Brüchen fällt vielen von uns schwer, weshalb ich im Folgenden das Berechnen von Brüchen bei einer Multiplikation, sowie Division erklären und erleichtern möchte.

Multiplikation von Brüchen:

Um euch effektiver helfen zu können, habe ich in diesem Video kurz erklärt, wie man richtig Brüche miteinander multipliziert→

Teste hier, ob du das Prinzip der Multiplikation von Brüchen verstanden hast:


Beim Multiplizieren von Brüche muss man Zähler mit Zähler und Nenner mit Nenner miteinander multiplizieren.



Division von Brüchen:

Hierbei spielt der Kehrwert eine große Rolle. Kehrwert heißt, dass der Zweite Bruch umgedreht wird, also→ Zähler und Nenner werden vertauscht. Nach der Umwandlung, ändert sich auch das Rechenzeichen, und das "÷" wird zu einem "·". Nun werden die 2 Brüche miteinander multipliziert und tadaaa, du hast die Lösung. Am Ende kannst du nochmal überprüfen, ob du das Ergebnis kürzen kannst. So schwer war das doch gar nicht oder?:)

Aber falls du es noch nicht ganz verstanden hast, habe ich hier ein Beispiel für dich:

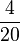  \frac{2}{4}   :   \frac{5}{2}   =   \frac{2}{4}  ·  \frac{2}{5}   =   \frac{4}{20}   =   \frac{1}{5}  
Von „https://projektwiki.zum.de/index.php?title=Julius-Echter-Gymnasium/Mathematik/Multiplikation_und_Division_von_Brüchen&oldid=32298“