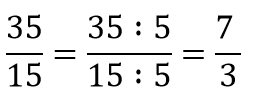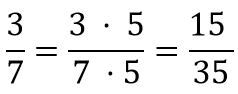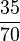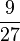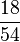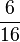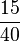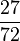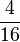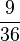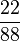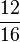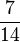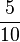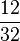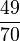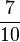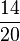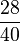Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Addition und Subtraktion ungleichnamiger Brüche: Unterschied zwischen den Versionen
| (35 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <u></u><div style="padding:50px;background: #EEEE00;border:0px groove;"> | ||
| + | |||
| + | <div style="margin:0; margin-right:50px; margin-left:50px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;"> | ||
| + | <big><span style="color:#9AFF9A"> | ||
| + | |||
<div style="padding:1px;background:#9AFF9A;border:0px groove;"> | <div style="padding:1px;background:#9AFF9A;border:0px groove;"> | ||
<colorize>Addition und Subtraktion ungleichnamiger Brüche</colorize> | <colorize>Addition und Subtraktion ungleichnamiger Brüche</colorize> | ||
| − | ''Definition'': <u>Ungleichnamige Brüche</u> | + | ''Definition'': <u>'''<span style="color: red">Ungleichnamige Brüche</span></u> |
Ungleichnamige Brüche sind Brüche, die '''<span style="color: red">unterschiedliche Nenner</span>''' haben. | Ungleichnamige Brüche sind Brüche, die '''<span style="color: red">unterschiedliche Nenner</span>''' haben. | ||
| − | Diese Brüche kannst du addieren oder subtrahieren, | + | Diese Brüche kannst du erst dann addieren oder subtrahieren, wenn du sie zuerst '''<span style="color: blue">auf den gleichen Nenner </span>'''gebracht hast. |
Hierfür musst du die Brüche zuerst erweitern oder kürzen. | Hierfür musst du die Brüche zuerst erweitern oder kürzen. | ||
| − | |||
| − | Du | + | <popup name= Erweitern/Kuerzen> |
| + | '''Wiederholung: '''<span style="color: blue">'''Kürzen'''</span>''' von Brüchen:''' | ||
| + | |||
| + | Du kürzt Brüche, indem du den Zähler und den Nenner durch '''<span style="color: blue">die gleiche Zahl dividierst.</span>''' | ||
Der Wert des Bruches bleibt hierbei unverändert. | Der Wert des Bruches bleibt hierbei unverändert. | ||
Beispiel: | Beispiel: | ||
| − | [[Datei: | + | [[Datei:A000Bruch.PNG|links|Bruch kürzen]] |
| − | + | ||
| − | + | ||
| − | + | ||
| Zeile 28: | Zeile 32: | ||
| − | ''' | + | '''Wiederholung: '''<span style="color: blue">'''Erweitern'''</span>''' von Brüchen:''' |
Du erweiterst Brüche, indem du den Zähler und den Nenner mit '''<span style="color: blue">der gleichen Zahl multiplizierst.</span>''' | Du erweiterst Brüche, indem du den Zähler und den Nenner mit '''<span style="color: blue">der gleichen Zahl multiplizierst.</span>''' | ||
| Zeile 35: | Zeile 39: | ||
Beispiel: | Beispiel: | ||
| − | [[Datei: | + | [[Datei:Brüche erweitern.PNG|links|Bruch erweitern]] |
| − | + | ||
| Zeile 42: | Zeile 45: | ||
Bei diesem Beispiel wurden sowohl der Zähler als auch der Nenner mit 5 multipliziert. | Bei diesem Beispiel wurden sowohl der Zähler als auch der Nenner mit 5 multipliziert. | ||
| + | <br /> | ||
| + | |||
| + | Eine ausführlichere Wiederholung zum Erweitern und Kürzen von Brüchen findest du hier: | ||
| + | [[Julius-Echter-Gymnasium/Mathematik/Erweitern_und_Kürzen|Erweitern und Kürzen]] | ||
| + | |||
| + | </popup> | ||
| + | |||
| + | |||
| + | |||
| + | '''<span style="color: green">Nachdem du alle Brüche auf den gleichen Nenner gebracht hast, kannst du die jetzt gleichnamigen Brüche wie gewohnt addieren oder subtrahieren. <br /> | ||
| + | Denk dran: <br /> | ||
| + | Du darfst nur die Zähler addieren bzw. subtrahieren. Die Nenner bleiben dabei immer gleich!</span>''' | ||
| − | |||
<popup name= Aufgaben > | <popup name= Aufgaben > | ||
| Zeile 55: | Zeile 69: | ||
| + | Kürze die Brüche in der unteren Leiste und ziehe sie zu ihrem vollständig gekürzten Partner. | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{| | {| | ||
| − | | '''<math>\frac{1}{2}</math>''' || '''<math>\frac{2}{4}</math>''' | + | | '''<math>\frac{1}{2}</math>''' || '''<math>\frac{2}{4}</math>''' || '''<math>\frac{3}{6}</math>''' || '''<math>\frac{35}{70}</math>''' |
|- | |- | ||
| − | | | + | | '''<math>\frac{1}{3}</math>''' || '''<math>\frac{3}{9}</math>''' || '''<math>\frac{9}{27}</math>''' || '''<math>\frac{18}{54}</math>''' |
|- | |- | ||
| − | | | + | | '''<math>\frac{3}{8}</math>''' || '''<math>\frac{6}{16}</math>''' || '''<math>\frac{15}{40}</math>''' || '''<math>\frac{27}{72}</math>''' |
| + | |- | ||
| + | | '''<math>\frac{1}{4}</math>''' || '''<math>\frac{4}{16}</math>''' || '''<math>\frac{9}{36}</math>''' || '''<math>\frac{22}{88}</math>''' | ||
|} | |} | ||
| Zeile 70: | Zeile 87: | ||
| + | Erweitere die Brüche in der unteren Leiste und ziehe sie zu ihrem Partner. | ||
| + | <div class="zuordnungs-quiz"> | ||
| + | |||
| + | {| | ||
| + | | '''<math>\frac{12}{16}</math>''' || '''<math>\frac{3}{4}</math>''' || '''<math>\frac{6}{8}</math>''' | ||
| + | |- | ||
| + | | '''<math>\frac{35}{70}</math>''' || '''<math>\frac{1}{2}</math>''' || '''<math>\frac{7}{14}</math>''' || '''<math>\frac{5}{10}</math>''' | ||
| + | |- | ||
| + | | '''<math>\frac{15}{40}</math>''' || '''<math>\frac{3}{8}</math>''' || '''<math>\frac{6}{16}</math>''' || '''<math>\frac{12}{32}</math>''' | ||
| + | |- | ||
| + | | '''<math>\frac{49}{70}</math>''' || '''<math>\frac{7}{10}</math>''' || '''<math>\frac{14}{20}</math>''' || '''<math>\frac{28}{40}</math>''' | ||
| + | |} | ||
| + | |||
| + | </div> | ||
| + | |||
| + | Brüche erweitern und kürzen | ||
| + | <iframe src="https://learningapps.org/watch?v=p3mk763hk18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | Ungleichnamige Brüche addieren und subtrahieren | ||
| + | <iframe src="https://learningapps.org/watch?v=pgkwvs8ma18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | |||
| + | Ungleichnamige Brüche addieren und subtrahieren | ||
| + | <iframe src="https://learningapps.org/watch?v=pdkc62ysk18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | Ungleichnamige Brüche addieren und subtrahieren | ||
| + | <iframe src="https://learningapps.org/watch?v=p4owud2aj18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| − | |||
| − | |||
</popup> | </popup> | ||
| + | |||
| + | |||
| + | |||
| + | {{Vorlage:Lesepfad Ende | ||
| + | |Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_gleichnamiger_Br%C3%BCche|zur Addition und Subtraktion gleichnamiger Brüche]] | ||
| + | |Link vor=[[Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_von_gemischten_Zahlen|zur Addition und Subtraktion von gemischten Zahlen]] | ||
| + | |Text Copyright= | ||
| + | }} | ||
Aktuelle Version vom 10. Januar 2020, 13:07 Uhr
Addition und Subtraktion ungleichnamiger Brüche
Definition: Ungleichnamige Brüche
Ungleichnamige Brüche sind Brüche, die unterschiedliche Nenner haben.
Diese Brüche kannst du erst dann addieren oder subtrahieren, wenn du sie zuerst auf den gleichen Nenner gebracht hast.
Hierfür musst du die Brüche zuerst erweitern oder kürzen.
Nachdem du alle Brüche auf den gleichen Nenner gebracht hast, kannst du die jetzt gleichnamigen Brüche wie gewohnt addieren oder subtrahieren.
Denk dran:
Du darfst nur die Zähler addieren bzw. subtrahieren. Die Nenner bleiben dabei immer gleich!
| zur Addition und Subtraktion gleichnamiger Brüche | zur Addition und Subtraktion von gemischten Zahlen |