Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).KW 09: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Wochenplan KW 9 == | + | === Wochenplan KW 9 === |
| + | <div style="margin:0px; margin-right:50px; border:thick double red; padding: 1em 1em 1em 1em; background-color:white; width:40%; align:center; "> | ||
| + | '''<span style="color:red">Besprechung Mi 07.03.</span>''' | ||
| + | * <span style="color:green">grüne Aufgaben </span> sind Pflichtaufgaben | ||
| + | * <span style="color:orange">orange Aufgaben </span> sind optional zur vertiefenden Übung | ||
| + | </div> | ||
<br /> | <br /> | ||
| − | + | ====<span style="color:green">Aufgabe I</span>==== | |
| − | + | Bestimme die Lösungen folgender Gleichungen.<br /> | |
| − | ==== | + | Denke an die binomischen Formeln! |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Bestimme die Lösungen folgender Gleichungen. | + | |
#) <math>x^2 + 15x + 56 = 0</math> | #) <math>x^2 + 15x + 56 = 0</math> | ||
| − | #) <math> | + | #) <math>x^2 = -10x - 25</math> |
#) <math>x^2 - 9x = 10</math> | #) <math>x^2 - 9x = 10</math> | ||
#) <math>x^2-25=0</math> | #) <math>x^2-25=0</math> | ||
| Zeile 20: | Zeile 17: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | ==== Aufgabe III ==== | + | ====<span style="color:green">Aufgabe II</span>==== |
| + | Bestimme rechnerisch, ob die Gleichungen eine, zwei oder keine Lösungen besitzen.<br /> | ||
| + | #) <math>2x^2-3x-5=0</math> | ||
| + | #) <math>5x^2=-9x-2</math> | ||
| + | #) <math>-x^2+6x=9</math> | ||
| + | #) <math>4x-2=7+9x</math> | ||
| + | #) <math>-x^2+5x-9=0</math> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ====<span style="color:green">Aufgabe III</span>==== | ||
| + | {| width="90%" | ||
| + | |width="30%" style="vertical-align:top" | | ||
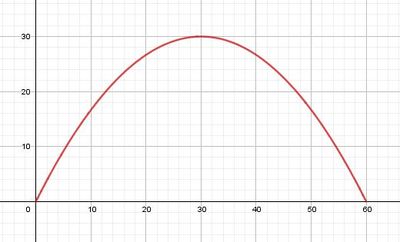
Der Sprung eines Frosches wird durch die Parabel <math>f(x)=-\frac{1}{30}x^2+2x</math> dargestellt. | Der Sprung eines Frosches wird durch die Parabel <math>f(x)=-\frac{1}{30}x^2+2x</math> dargestellt. | ||
#) Bestimme wie weit der Frosch springt. | #) Bestimme wie weit der Frosch springt. | ||
#) Berechne nach welcher Weite er die Höhe <math>h=\frac{45}{2}</math> erreicht hat. | #) Berechne nach welcher Weite er die Höhe <math>h=\frac{45}{2}</math> erreicht hat. | ||
| + | | width="10%" style="vertical-align:top" | | ||
| + | | width="50%" style="vertical-align:top" | | ||
| + | [[Datei:Froschsprung.JPG|400px|Geometrische Veranschaulichung; Froschsprung]] | ||
| + | |} | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | ==== Aufgabe IV ==== | + | ====<span style="color:orange">Aufgabe IV</span>==== |
| − | Ein Rechteck hat einen Umfang von 78cm und einen Flächeninhalt von 324cm². | + | Ein Rechteck mit den Seitenlängen ''a'' und ''b'' hat einen Umfang von 78cm und einen Flächeninhalt von 324cm². |
| − | Berechne die Seitenlängen a und b. | + | Berechne die Seitenlängen ''a'' und ''b''. |
| + | <br /> | ||
| + | Lösung: {{versteckt|<math>a=12</math>, <math>b=27</math>}} | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ---- | ||
| + | <br /> | ||
| + | ====Lösungen der Aufgaben aus KW 9:<br />==== | ||
| + | {| | ||
| + | |width="33%"| [[Datei:KW 9 Lösung 1.jpg|thumb|links|Lösungen der Aufgaben aus KW 9 Blatt 1]] | ||
| + | |width="33%"| [[Datei:KW 9 Lösung 2.jpg|thumb|links|Lösungen der Aufgaben aus KW 9 Blatt 2]] | ||
| + | |width="33%"| [[Datei:KW 9 Lösung 3.jpg|thumb|links|Lösungen der Aufgaben aus KW 9 Blatt 3]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | <br /> | ||
| + | ---- | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <iframe src="https://learningapps.org/watch?v=pfk90i4wc18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
Aktuelle Version vom 18. April 2018, 21:44 Uhr
Inhaltsverzeichnis |
Wochenplan KW 9
Besprechung Mi 07.03.
- grüne Aufgaben sind Pflichtaufgaben
- orange Aufgaben sind optional zur vertiefenden Übung
Aufgabe I
Bestimme die Lösungen folgender Gleichungen.
Denke an die binomischen Formeln!
- )
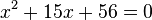
- )
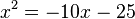
- )
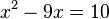
- )
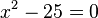
- )
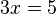
- )
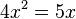
Aufgabe II
Bestimme rechnerisch, ob die Gleichungen eine, zwei oder keine Lösungen besitzen.
- )
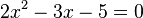
- )
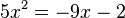
- )
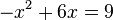
- )
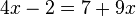
- )
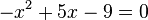
Aufgabe III
|
Der Sprung eines Frosches wird durch die Parabel
|
Aufgabe IV
Ein Rechteck mit den Seitenlängen a und b hat einen Umfang von 78cm und einen Flächeninhalt von 324cm².
Berechne die Seitenlängen a und b.
Lösung:
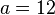 ,
, 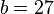
Lösungen der Aufgaben aus KW 9:
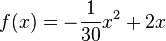 dargestellt.
dargestellt.
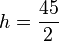 erreicht hat.
erreicht hat.