Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Bruchfunktionen: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
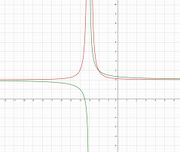
Bestimme den Funktionsterm einer Bruchfunktion mithilfe der gegebenen Asymptoten. Gib jeweils zwei unterschiedliche Funktionen an und skizziere die Funktionsgraphen dazu! | Bestimme den Funktionsterm einer Bruchfunktion mithilfe der gegebenen Asymptoten. Gib jeweils zwei unterschiedliche Funktionen an und skizziere die Funktionsgraphen dazu! | ||
<br /> | <br /> | ||
| − | + | {| | |
| + | |- | ||
| + | | 1.) <math>y=1, x=2</math> | ||
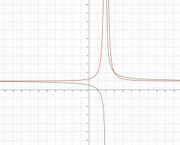
Lösung: {{versteckt|<math>f(x)=\frac{1}{x-2}+1</math> (grün), <math>g(x)=\frac{1}{(x-2)^2}+1</math> (rot) | Lösung: {{versteckt|<math>f(x)=\frac{1}{x-2}+1</math> (grün), <math>g(x)=\frac{1}{(x-2)^2}+1</math> (rot) | ||
<br /> | <br /> | ||
[[Datei:Bruchfunktion.JPG|thumb|left|Funktionsgraphen zweier Bruchfunktionen mit gleichen Asymptoten]] | [[Datei:Bruchfunktion.JPG|thumb|left|Funktionsgraphen zweier Bruchfunktionen mit gleichen Asymptoten]] | ||
}} | }} | ||
| − | + | |- | |
| − | + | |2.) <math>y=2, x=-3</math> | |
| − | + | ||
Lösung: {{versteckt|<math>f(x)=\frac{1}{x+3}+2</math> (grün), <math>g(x)=\frac{1}{(x+3)^2}+2</math> (rot) | Lösung: {{versteckt|<math>f(x)=\frac{1}{x+3}+2</math> (grün), <math>g(x)=\frac{1}{(x+3)^2}+2</math> (rot) | ||
<br /> | <br /> | ||
[[Datei:Bruchfunktion 2.JPG|thumb|left|Funktionsgraphen zweier Bruchfunktionen mit gleichen Asymptoten]] | [[Datei:Bruchfunktion 2.JPG|thumb|left|Funktionsgraphen zweier Bruchfunktionen mit gleichen Asymptoten]] | ||
}} | }} | ||
| + | |} | ||
Aktuelle Version vom 27. März 2018, 13:53 Uhr
Aufgabe 1: Zuordnungen
Ordne die Graphen mit den zusammengehörigen Funktionstermen.
Aufgabe 2: Zahlenstrahl
Ordne die Bilder der Graphen bzw. Funktionen an die Stellen des Zahlenstrahls, wo ihre Definitionslücken liegen.
Aufgabe 3: Funktionsterm aufstellen
Bestimme den Funktionsterm einer Bruchfunktion mithilfe der gegebenen Asymptoten. Gib jeweils zwei unterschiedliche Funktionen an und skizziere die Funktionsgraphen dazu!
1.) 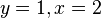
Lösung: |
2.) 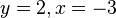
Lösung: |
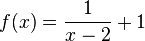 (grün),
(grün), 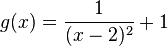 (rot)
(rot)
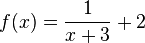 (grün),
(grün), 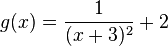 (rot)
(rot)