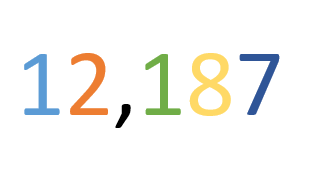Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Addition und Subtraktion von Dezimalzahlen: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
 
(6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
<u></u><div style="padding:50px;background:#B1FB17;border:0px groove;">
  
 +
<div style="margin:0; margin-right:50px; margin-left:50px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;">
  
−
<div style="padding:1px;background:#B1FB17;border:0px groove;">
+
Beim '''Addieren''' und '''Subtrahieren''' von '''Dezimalzahlen''' ist das Wichtigste, dass du die Kommas direkt untereinander schreibst.
  
−
Beim '''Addieren''' und '''Subtrahieren''' von '''Dezimalzahlen''' ist das wichtigste,dass die Kommas direkt untereinander stehen.
+
Die Ziffern vor dem Komma (Einer, Zehner, Hunderter, ...) müssen so wie die Ziffern hinter dem Komma (Zehntel, Hundertstel, Tausendstel,...)ebenfalls '''genau''' untereinander stehen.
  
−
Die Ziffern vor dem Komma (Einer,Zehner,Hunderter,...) müssen so wie die Ziffern hinter dem Komma (Zehntel,Hundertstel,Tausendstel,...) '''genau''' untereinander stehen.
+
Tipp: Wenn eine Zahl weniger Nachkommastellen hat als die andere, kannst du bei der kürzeren Zahl die hintersten Stellen mit Nullern ergänzen. Dann kannst du die Zahlen stellenweise wie gewohnt addieren und subtrahieren.
−
 
+
−
Tipp: Wenn eine Zahl kürzer ist als die andere werden die Stellen nach dem Komma mit einer 0 ergänzt.Dann kannst du die Zahlen stellenweise wie gewohnt addieren und subtrahieren.
+
  
 
* Beispiel Dezimalbruch:
 
* Beispiel Dezimalbruch:
−
 
−
 
  
  
 
[[Datei:Dezimalbruch 1.PNG|200px|gerahmt|zentriert]]
 
[[Datei:Dezimalbruch 1.PNG|200px|gerahmt|zentriert]]
  
−
  Die <span style="color: turquoise ">1</span> entspricht in diesem Beispiel der '''Zehnerstelle'''
+
  Die <span style="color: turquoise ">1</span> entspricht in diesem Beispiel der '''Zehnerstelle'''.
−
  Die <span style="color: orange ">2</span> entspricht in diesem Beispiel der '''Einerstelle'''
+
  Die <span style="color: orange ">2</span> entspricht in diesem Beispiel der '''Einerstelle'''.
−
  Die <span style="color: green ">1</span> entspricht in diesem Beispiel der '''Zehntelstelle'''
+
  Die <span style="color: green ">1</span> entspricht in diesem Beispiel der '''Zehntelstelle'''.
−
  Die <span style="color: #FFD801">8</span> entspricht in diesem Beispiel der '''Hundertstelstelle'''
+
  Die <span style="color: #FFD801">8</span> entspricht in diesem Beispiel der '''Hundertstelstelle'''.
−
  Die <span style="color: darkblue ">7</span> entspricht in diesem Beispiel der '''Tausendstelstelle'''
+
  Die <span style="color: darkblue ">7</span> entspricht in diesem Beispiel der '''Tausendstelstelle'''.
  
−
* Werden also zwei untereinander stehende '''Dezimalbrüche''' addiert fängt man bei der letzten Ziffernstelle der Dezimalbrüche an und addiert die untereinander stehenden Ziffern.
 
  
 +
* Werden also zwei untereinander stehende '''Dezimalbrüche''' addiert, fängt man bei der letzten Ziffernstelle der Dezimalbrüche an und addiert die untereinander stehenden Ziffern. Das Komma musst du natürlich auch übernehmen.
  
 
'''Beispiel 1 Addition''':  
 
'''Beispiel 1 Addition''':  
−
 
  
 
   13,423
 
   13,423
Zeile 32: Zeile 29:
 
   ------
 
   ------
 
   36,944
 
   36,944
−
 
−
* Ergibt sich dabei eine Zahl,die '''größer als 10 ist''' (zum Beispiel 13) wird die letzte Ziffer,in diesem Fall die 5 stehen gelassen und die 1 wird zu der '''nächst größeren Ziffernstelle''' dazu addiert.
 
  
  
 +
* Ergibt sich dabei eine Zahl, die '''größer als 10 ist''' (zum Beispiel 13) wird die letzte Ziffer, in diesem Fall die 3, stehen gelassen und die 1 wird zu der '''nächst größeren Ziffernstelle''' dazu addiert.
  
 
'''Beispiel 2 Addition''':
 
'''Beispiel 2 Addition''':
−
 
  
 
   14,829
 
   14,829
Zeile 45: Zeile 40:
 
   ------
 
   ------
 
   38,193
 
   38,193
 +
  
  
 
'''<u>Übungen zur Addition von Dezimalzahlen:</u>'''
 
'''<u>Übungen zur Addition von Dezimalzahlen:</u>'''
 
<br />
 
<br />
 +
 +
<u>Aufgabe 1</u>
  
 
<popup name= Aufgabe 1>
 
<popup name= Aufgabe 1>
Zeile 56: Zeile 54:
 
</popup>
 
</popup>
  
 +
 +
 +
<u>Aufgabe 2</u>
  
 
<popup Name= Aufgabe 2>
 
<popup Name= Aufgabe 2>
Zeile 63: Zeile 64:
 
</popup>
 
</popup>
  
 +
 +
 +
<u>Aufgabe 3</u>
  
 
<popup Name= Aufgabe 3>
 
<popup Name= Aufgabe 3>
Zeile 71: Zeile 75:
  
  
 +
 +
<u>Aufgabe 4</u>
  
 
<popup Name= Aufgabe 4>
 
<popup Name= Aufgabe 4>
Zeile 81: Zeile 87:
  
  
−
* Werden zwei untereinander stehende '''Dezimalbrüche''' subtrahiert fängt man bei der letzten Ziffernstelle der Dezimalbrüche an und subtrahiert die ''untere'' von der ''oberen'' Zahl.  
+
* Werden zwei untereinander stehende '''Dezimalbrüche''' subtrahiert, fängt man bei der letzten Ziffernstelle der Dezimalbrüche an und subtrahiert die ''untere'' von der ''oberen'' Zahl.  
−
 
+
−
* Ist die untere Ziffer '''größer''' als die obere wird von der nächst größeren Ziffernstelle eine 1 weggenommen und zur oberen Zahl hinzugefügt.
+
−
 
+
  
 
'''Beispiel 1 Subtraktion'''
 
'''Beispiel 1 Subtraktion'''
−
 
  
 
   65,875
 
   65,875
Zeile 94: Zeile 96:
 
   33,243
 
   33,243
  
 +
 +
* Ist die untere Ziffer '''größer''' als die obere, wird von der nächst größeren Ziffernstelle eine 1 weggenommen und zur oberen Zahl hinzugefügt.
  
 
'''Beispiel 2 Subtraktion'''
 
'''Beispiel 2 Subtraktion'''
Zeile 107: Zeile 111:
  
 
<u>'''Übungen zur Subtraktion von Dezimalzahlen'''</u>
 
<u>'''Übungen zur Subtraktion von Dezimalzahlen'''</u>
−
<popup name= Aufgabe>
 
  
−
<iframe src="https://learningapps.org/watch?v=pvqbscw8j18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
<u>Aufgabe 1</u>
  
 +
<popup name= Aufgabe 1>
 +
 +
<iframe src="https://learningapps.org/watch?v=p542t3f8518" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
  
 
</popup>
 
</popup>
  
 +
 +
<u>Aufgabe 2</u>
  
 
<popup name= Aufgabe 2>
 
<popup name= Aufgabe 2>
  
−
<iframe src="https://learningapps.org/watch?v=p542t3f8518" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
<iframe src="https://learningapps.org/watch?v=pi9qdw6zj18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
  
 
</popup>
 
</popup>
  
 +
 +
<u>Aufgabe 3</u>
  
 
<popup name= Aufgabe 3>
 
<popup name= Aufgabe 3>
  
−
<iframe src="https://learningapps.org/watch?v=pi9qdw6zj18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
<iframe src="https://learningapps.org/watch?v=p2aay5rrk18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
  
 
</popup>
 
</popup>
  
  
−
<popup name= Aufgabe 4>
 
−
 
−
<iframe src="https://learningapps.org/watch?v=p2aay5rrk18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
 
−
 
−
</popup>
 
  
 
{{Vorlage:Lesepfad Ende
 
{{Vorlage:Lesepfad Ende
 
|Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_von_gemischten_Zahlen|zur Addition und Subtraktion von gemischten Zahlen]]                   
 
|Link zurück=[[Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_von_gemischten_Zahlen|zur Addition und Subtraktion von gemischten Zahlen]]                   
−
|Link vor=[[Julius-Echter-Gymnasium/Mathematik|zurück zum Inhaltsverzeichnis]]
+
|Link vor=[[Julius-Echter-Gymnasium/Mathematik/Multiplikation_von_Brüchen|zur Multiplikation von Brüchen]]
 
|Text Copyright=
 
|Text Copyright=
 
}}
 
}}
−
 
−
 
−
<div style="padding:1px;background:#B1FB17;border:0px groove;">
 

Aktuelle Version vom 12. Januar 2020, 15:16 Uhr

Beim Addieren und Subtrahieren von Dezimalzahlen ist das Wichtigste, dass du die Kommas direkt untereinander schreibst.

Die Ziffern vor dem Komma (Einer, Zehner, Hunderter, ...) müssen so wie die Ziffern hinter dem Komma (Zehntel, Hundertstel, Tausendstel,...)ebenfalls genau untereinander stehen.

Tipp: Wenn eine Zahl weniger Nachkommastellen hat als die andere, kannst du bei der kürzeren Zahl die hintersten Stellen mit Nullern ergänzen. Dann kannst du die Zahlen stellenweise wie gewohnt addieren und subtrahieren.

  • Beispiel Dezimalbruch:


Dezimalbruch 1.PNG 
Die 1 entspricht in diesem Beispiel der Zehnerstelle.
Die 2 entspricht in diesem Beispiel der Einerstelle.
Die 1 entspricht in diesem Beispiel der Zehntelstelle.
Die 8 entspricht in diesem Beispiel der Hundertstelstelle.
Die 7 entspricht in diesem Beispiel der Tausendstelstelle.


  • Werden also zwei untereinander stehende Dezimalbrüche addiert, fängt man bei der letzten Ziffernstelle der Dezimalbrüche an und addiert die untereinander stehenden Ziffern. Das Komma musst du natürlich auch übernehmen.

Beispiel 1 Addition: 

 13,423
+23,521
 ------
 36,944


  • Ergibt sich dabei eine Zahl, die größer als 10 ist (zum Beispiel 13) wird die letzte Ziffer, in diesem Fall die 3, stehen gelassen und die 1 wird zu der nächst größeren Ziffernstelle dazu addiert.

Beispiel 2 Addition: 

 14,829
+23,364
  1  1
 ------
 38,193


Übungen zur Addition von Dezimalzahlen:

Aufgabe 1


Aufgabe 2


Aufgabe 3


Aufgabe 4



  • Werden zwei untereinander stehende Dezimalbrüche subtrahiert, fängt man bei der letzten Ziffernstelle der Dezimalbrüche an und subtrahiert die untere von der oberen Zahl.

Beispiel 1 Subtraktion 

 65,875
-32,632
 ------
 33,243


  • Ist die untere Ziffer größer als die obere, wird von der nächst größeren Ziffernstelle eine 1 weggenommen und zur oberen Zahl hinzugefügt.

Beispiel 2 Subtraktion 

              11
 28,239    27,139
-15,543 = -15,543
           ------
           12,696



Übungen zur Subtraktion von Dezimalzahlen

Aufgabe 1


Aufgabe 2


Aufgabe 3


zur Addition und Subtraktion von gemischten Zahlen zur Multiplikation von Brüchen

Von „https://projektwiki.zum.de/index.php?title=Julius-Echter-Gymnasium/Mathematik/Addition_und_Subtraktion_von_Dezimalzahlen&oldid=80438“