Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Brüche als Quotienten: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<u></u><div style="padding:50px;background: #0000FF;border:0px groove;"> | <u></u><div style="padding:50px;background: #0000FF;border:0px groove;"> | ||
| − | + | <div style="margin:0; margin-right:50px; margin-left:50px; border:5px solid #FFFFFF; padding: 1em 1em 1em 1em; background-color:#FFFFFF; align:left;"> | |
| − | + | ||
| − | <div style="margin:0; margin-right: | + | |
<big><span style="color:#C00000"> | <big><span style="color:#C00000"> | ||
| − | |||
| − | |||
<div style="padding:1px;background:;border:0px groove;"> | <div style="padding:1px;background:;border:0px groove;"> | ||
<colorize>Brüche als Quotienten</colorize> | <colorize>Brüche als Quotienten</colorize> | ||
| − | |||
| − | |||
In der Mathematik bezeichnet der '''Quotient''' ein '''Verhältnis''' von zwei Größen zueinander, also das Ergebnis einer ''Division''. Der Quotient von zwei ganzen Zahlen (Dividend und Divisor) ist immer eine rationale Zahl und kann als Bruch geschrieben werden. | In der Mathematik bezeichnet der '''Quotient''' ein '''Verhältnis''' von zwei Größen zueinander, also das Ergebnis einer ''Division''. Der Quotient von zwei ganzen Zahlen (Dividend und Divisor) ist immer eine rationale Zahl und kann als Bruch geschrieben werden. | ||
| − | Den | + | Den '''Quotienten z:n''' zweier natürlicher Zahlen kann man auch als '''Bruch <math> \frac{z}{n}</math>''' schreiben. |
<u>Ein Beispiel:</u> 3:7 = <math> \frac{3}{7}</math> oder 5:9 = <math> \frac{5}{9}</math> | <u>Ein Beispiel:</u> 3:7 = <math> \frac{3}{7}</math> oder 5:9 = <math> \frac{5}{9}</math> | ||
| Zeile 24: | Zeile 18: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | Welcher Bruch | + | Welcher Bruch entspricht der Divisionsaufgabe '''6:9''' ? (!<math> \frac{9}{6}</math>) (<math> \frac{6}{9}</math>) |
| + | |||
| + | Welcher Bruch entspricht der Divisionsaufgabe '''3:8''' ? (!<math> \frac{8}{3}</math>) (<math> \frac{3}{8}</math>) | ||
| + | |||
| + | Welcher Bruch entspricht der Divisionsaufgabe '''17:4''' ? (!<math> \frac{4}{17}</math>) (<math> \frac{17}{4}</math>) | ||
| + | |||
</div> | </div> | ||
| Zeile 35: | Zeile 34: | ||
| − | Nun gibt es hier für dich | + | Nun gibt es hier für dich noch ein paar Übungen zu dem Thema ''Brüche als Quotienten''. '''Viel Spaß'''! |
| − | + | ||
| + | <u>Aufgabe 1</u> | ||
<popup name= Aufgabe> | <popup name= Aufgabe> | ||
<iframe src="https://learningapps.org/watch?v=p1oiqeecn18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=p1oiqeecn18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| Zeile 44: | Zeile 43: | ||
| − | + | <u>Aufgabe 2</u> | |
| + | <popup name= Aufgabe> | ||
| + | <iframe src="https://learningapps.org/watch?v=ptsj0hqm318" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | </popup> | ||
| + | |||
| + | <u>Aufgabe 3</u> | ||
<popup name= Aufgabe> | <popup name= Aufgabe> | ||
| − | <iframe src="https://learningapps.org/watch?v= | + | <iframe src="https://learningapps.org/watch?v=p6axgzwh318" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
</popup> | </popup> | ||
Aktuelle Version vom 9. Januar 2020, 12:02 Uhr
Brüche als Quotienten
In der Mathematik bezeichnet der Quotient ein Verhältnis von zwei Größen zueinander, also das Ergebnis einer Division. Der Quotient von zwei ganzen Zahlen (Dividend und Divisor) ist immer eine rationale Zahl und kann als Bruch geschrieben werden.
Den Quotienten z:n zweier natürlicher Zahlen kann man auch als Bruch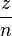 
schreiben.
Ein Beispiel: 3:7 = 
oder 5:9 = 
Multiplechoice-Quiz
|
Welcher Bruch entspricht der Divisionsaufgabe 6:9 ? (! Welcher Bruch entspricht der Divisionsaufgabe 3:8 ? (! Welcher Bruch entspricht der Divisionsaufgabe 17:4 ? (! |
) (
)
) (
)
) (
)
Nun gibt es hier für dich noch ein paar Übungen zu dem Thema Brüche als Quotienten. Viel Spaß!
Aufgabe 1
Aufgabe 2
Aufgabe 3
| zum Erweitern und Kürzen | zu Dezimalbrüchen |
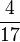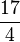