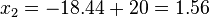Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Quadratische Funktionen: Unterschied zwischen den Versionen
(→Von der Normalform zur Scheitelpunktform) |
K (Maria Eirich verschob Seite DiWerS/Funktioniert's? Übergang von der SI zur SII/Quadratische Funktionen nach Digitale Werkzeuge in der Schule/Funktioniert's? Übergang von der SI zur SII/Quadratische Funktionen) |
||
| (124 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 20: | Zeile 20: | ||
{{Aufgaben|3 Zeichnen von Graphen anhand der Scheitelpunktform| | {{Aufgaben|3 Zeichnen von Graphen anhand der Scheitelpunktform| | ||
| − | Skizziere die angegebenen Funktionen als Graphen | + | Skizziere die angegebenen Funktionen als Graphen in dein Heft:<br /> |
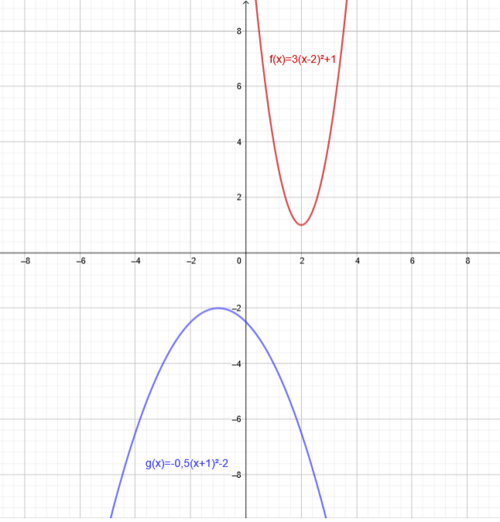
<math>1.\quad f(x)=3(x-2)^2+1</math> <br /> | <math>1.\quad f(x)=3(x-2)^2+1</math> <br /> | ||
| Zeile 64: | Zeile 64: | ||
== Scheitelpunktform und Normalform == | == Scheitelpunktform und Normalform == | ||
| − | {{Aufgaben|5 Rechnen mit der Scheitelpunktform und der Normalform| | + | {{Aufgaben|5 Rechnen mit der Scheitelpunktform und der Normalform|Fülle den Lückentext aus, indem du in die Lücken klickst und die richtige Antwort auswählst. |
| + | <iframe src="https://learningapps.org/watch?app=5077950" style="border:0px;width:100%;height:720px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}}<br /> | ||
<br /> | <br /> | ||
=== Von der Scheitelpunktform zur Normalform === | === Von der Scheitelpunktform zur Normalform === | ||
| − | {{Aufgaben|6 Umformung von der Scheitelpunktform zur Normalform|Forme die folgenden Scheitelpunktformen in deinem Heft in die Normalenformen um und klicke dann das richtige Ergebnis an.<iframe src="https://learningapps.org/watch?v=p4jtn4wkk18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | + | {{Aufgaben|6 Umformung von der Scheitelpunktform zur Normalform|Forme die folgenden Scheitelpunktformen in deinem Heft in die Normalenformen um und klicke dann das richtige Ergebnis an.<iframe src="https://learningapps.org/watch?v=p4jtn4wkk18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
<popup name="Tipp 1"> | <popup name="Tipp 1"> | ||
Benutze zum Lösen die 1. oder 2. Binomische Formel! | Benutze zum Lösen die 1. oder 2. Binomische Formel! | ||
| Zeile 114: | Zeile 115: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| − | </popup> | + | </popup>}} |
| − | + | ||
=== Von der Normalform zur Scheitelpunktform === | === Von der Normalform zur Scheitelpunktform === | ||
| Zeile 127: | Zeile 127: | ||
Wir wollen jetzt also nicht die Klammer ausmultiplizieren, sondern den Term zu so einem Klammerausdruck umformen, z.B. den Term <math>x^2+6x+15</math>. <br> | Wir wollen jetzt also nicht die Klammer ausmultiplizieren, sondern den Term zu so einem Klammerausdruck umformen, z.B. den Term <math>x^2+6x+15</math>. <br> | ||
Wie das funktioniert, kannst du in dieser Aufgabe noch mal wiederholen: | Wie das funktioniert, kannst du in dieser Aufgabe noch mal wiederholen: | ||
| − | {{Aufgaben|7 Die quadratische Ergänzung wiederholen| | + | {{Aufgaben|7 Die quadratische Ergänzung wiederholen|'''Wichtig''': Wenn for dem x<sup>2</sup> ein Faktor steht, muss dieser zunächst ausgeklammert werden. |
| − | <iframe src="https://learningapps.org/watch?app=5233722" style="border:0px;width: | + | <iframe src="https://learningapps.org/watch?app=5233722" style="border:0px;width:70%;height:900px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}} |
| − | |||
{{Aufgaben|8 Quadratische Ergänzung bei Vorfaktor|Ergänze in dem folgenden Beispiel die Umformungsschritte, indem du sie an die richtige Stelle ziehst.}} | {{Aufgaben|8 Quadratische Ergänzung bei Vorfaktor|Ergänze in dem folgenden Beispiel die Umformungsschritte, indem du sie an die richtige Stelle ziehst.}} | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 143: | Zeile 142: | ||
| − | {{Aufgaben|9 Umformung von der Normalform zur Scheitelpunktform|<iframe src="https://learningapps.org/watch?app=5078271" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | + | {{Aufgaben|9 Umformung von der Normalform zur Scheitelpunktform|<iframe src="https://learningapps.org/watch?app=5078271" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
<popup name="Tipp"> | <popup name="Tipp"> | ||
| Zeile 150: | Zeile 149: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | < | + | <math>f(x):</math> |
| − | <math> | + | {{Lösung versteckt mit Rand|1=<math> |
\begin{array}{rll} | \begin{array}{rll} | ||
f(x)&=&x^2-8x+18 | f(x)&=&x^2-8x+18 | ||
| Zeile 158: | Zeile 157: | ||
\\ &=&(x-4)^2+2 \\ | \\ &=&(x-4)^2+2 \\ | ||
\end{array} | \end{array} | ||
| − | </math> | + | </math>}} |
| − | + | ||
| − | < | + | <math>g(x):</math> |
| + | {{Lösung versteckt mit Rand|1= | ||
| + | <math> | ||
\begin{array}{rll} | \begin{array}{rll} | ||
g(x)&=&5x^2+30x+43 \\ &=&5(x^2+6x+8.6) \\ &=&5(x^2+6x+3^2-3^2+8.6) \\ &=&5[(x+3)^2-3^2+8.6] \\ &=&5[(x+3)^2-0.4] \\ &=&5(x+3)^2-2 | g(x)&=&5x^2+30x+43 \\ &=&5(x^2+6x+8.6) \\ &=&5(x^2+6x+3^2-3^2+8.6) \\ &=&5[(x+3)^2-3^2+8.6] \\ &=&5[(x+3)^2-0.4] \\ &=&5(x+3)^2-2 | ||
\end{array} | \end{array} | ||
| − | </math> | + | </math>}} |
| − | < | + | <math>h(x):</math> |
| + | {{Lösung versteckt mit Rand|1= | ||
<math> | <math> | ||
\begin{array}{rll} | \begin{array}{rll} | ||
| Zeile 175: | Zeile 176: | ||
\\ &=&0.2(x-1.5)^2 | \\ &=&0.2(x-1.5)^2 | ||
\end{array} | \end{array} | ||
| − | </math> | + | </math>}} |
| − | </popup> | + | </popup>}} |
| − | == Anwendungsaufgabe " | + | == Anwendungsaufgabe "Rakete" == |
| − | {{Aufgaben| | + | {{Aufgaben|10 Rakete|Zum Abschluss eines Volksfestes wird ein Feuerwerk vom Dach eines Parkhauses abgeschossen. Der Pyrotechniker hat für die Beschreibung der Flugbahn einer Rakete die Funktion <br><math>f(x)=-0.2x^2+8x+18</math> <br> aufgestellt. Dabei entspricht <math>x</math> der horizontalen Entfernung von der Abschussstelle und <math>f(x)</math> der Höhe der Rakete; jeweils in Meter.<br /><br /> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <popup name=" | + | a) Berechne <math>f(0)</math> und beschreibe, was dieser Wert im Anwendungskontext bedeutet.<br /> |
| − | + | <popup name="Tipp"> Lies noch einmal nach, was <math>x</math> und <math>f(x)</math> angeben. Was bedeutet es, wenn <math>x=0</math> ist? </popup><br /> | |
| + | |||
| + | b) Berechne, wie weit die Rakete fliegen würde, bis sie auf den Boden auftrifft. <br /> | ||
| + | <popup name="Tipp 1"> Überlege dir, welchen Wert <math>f(x)</math> annehmen muss, wenn die Rakete auf den Boden auftritt. </popup> | ||
| + | <popup name="Tipp 2"> Setze <math>f(x)=0</math> und berechne die Nullstellen mithilfe der p-q-Formel. </popup> | ||
| + | <popup name="Tipp 3"> '''Die p-q-Formel:'''Für eine Gleichung <math>0=x^2+px+q</math> liefert die p-q-Formel die Lösungen<br /> | ||
<math> | <math> | ||
| − | + | x_{1/2}= -\frac{p}{2} \pm \sqrt{{\left ( \frac{p}{2} \right )}^2 -q} | |
| − | + | </math>.<br> Denke daran, dass dabei vor dem <math>x^2</math> kein Vorfaktor stehten darf. Diesen kann man eliminieren, indem man auf beiden Seiten der Gleichung durch den Vorfaktor teilt.<br> | |
| − | + | </popup><br /> | |
| − | \ | + | |
| − | </math> <br> | + | |
| − | </popup> | + | c) Nach wieviel Metern erreicht die Rakete ihre maximale Höhe? Welche Höhe erreicht sie?<br /> |
| − | <popup name=" | + | <popup name="Tipp 1"> Gesucht ist der Scheitelpunkt der Funktion. Erinnere dich daran, wo man den Scheitelpunkt ablesen kann. </popup> |
| − | + | <popup name="Tipp 2"> Wenn du nicht weiterweißt, schaue in den Aufgaben 7, 8 und 9 noch einmal nach. </popup><br /> | |
| + | |||
| + | d) Bei gleichbleibendem Startpunkt soll die Flugbahn so verändert werden, dass nach 10 m Entfernung vom Startpunkt die maximale Höhe von 120 m erreicht wird. Bestimme eine Funktionsgleichung für diese neue Flugbahn. | ||
| + | <popup name="Tipp 1"> Stelle die Gleichung mit Hilfe des Scheitelpunktes <math> S(10\mid120)</math> und des Punktes <math>P(0\mid18)</math> auf.</popup> | ||
| + | <popup name="Tipp 2"> Gehe wie in Aufgabe 4 vor. </popup><br /> | ||
| + | |||
| + | Zusatzaufgabe* Berechne die horizontale Entfernung vom Startpunkt, in der die Rakete theoretisch eine Flughöhe von 30 m hat. | ||
| + | <popup name="Tipp"> Gesucht sind die x-Werte, für die <math>f(x)=30</math> ist. </popup> | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | a) | ||
| + | {{Lösung versteckt mit Rand| | ||
<math> | <math> | ||
\begin{array}{rll} | \begin{array}{rll} | ||
| − | f( | + | f(0)&=&-0.2 \cdot 0^2+8 \cdot 0+18 \\ |
| − | \end{array} | + | &=& 18 |
| − | </math> | + | \end{array} |
| − | <br | + | </math> <br> Das Dach, von dem die Rakete abgeschossen wird, ist 18 Meter hoch. }} |
| − | + | <br> | |
| − | + | b) | |
| − | </ | + | {{Lösung versteckt mit Rand| |
| − | < | + | Nullstellenberechnung:<br /> |
| − | + | Dafür müssen wir im ersten Schritt beim Summanden <math>x^2</math> den Vorfaktor eliminieren.<br /> | |
| − | + | ||
| − | + | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
| − | 0 | + | 0 & = & -0.2x^2+8x+18 & \mid :-0.2 \\ |
| − | &=&-0 | + | &=& x^2-40x-90 |
| − | &=&x^2- | + | |
\end{array} | \end{array} | ||
| − | + | </math><br /> | |
| − | </math> | + | Im zweiten Schritt benutzen wir die '''p-q-Formel''', um die Nullstellen der Funktion zu bestimmen.<br /> |
| − | <math> \Rightarrow p=- | + | <math> \Rightarrow p=-40, q=-90 </math> <br> |
<math> | <math> | ||
\begin{array}{rll} | \begin{array}{rll} | ||
| − | x_{1/2} &=& -\frac{- | + | x_{1/2} &=& -\frac{-40}{2} \pm \sqrt{{\left ( \frac{-40}{2} \right )}^2 -(-90)} \\ |
| − | &=& | + | &=& 20 \pm 22.14 \\ |
\end{array} | \end{array} | ||
| − | </math><br> | + | </math><br /> |
<math> | <math> | ||
| − | \Rightarrow x_1= | + | \Rightarrow x_1=22.14+20=42.14 </math> und <math> x_2=-22.14+20=-2.14 |
| − | </math> | + | </math><br /> |
| + | Da wir wissen wollen, wie weit die Rakete fliegen würde, bis sie auf dem Boden aufkommt, müssen wir nur den größeren x-Wert betrachten. Also kommt die Rakete nach ca. 42.14 Metern auf dem Boden auf.}} | ||
| + | c) | ||
| + | {{Lösung versteckt mit Rand| | ||
| + | Umwandeln in die Scheitelpunktform: <br /> | ||
| + | <math> | ||
| + | \begin{array}{rlll} | ||
| + | f(x) & = & -0.2x^2+8x+18 &\mid -0.2 \, vorklammern \\ | ||
| + | &=& -0.2(x^2-40x-90) &\mid quadratische \, Erg\ddot{a} nzung +20^2-20^2 \\ | ||
| + | &=& -0.2(x^2-2 \cdot 20x+20^2-20^2-90) & \mid 2. Binomische \, Formel \\ | ||
| + | &=& -0.2[(x-20)^2-490] & \mid ausmultiplizieren \\ | ||
| + | &=& -0.2 (x-20)^2+98 | ||
| + | \end{array} | ||
| + | </math><br /> | ||
| + | Der Scheitelpunkt liegt bei <math>S(20\mid 98)</math>, die maximale Höhe von 98 Metern wird also bei einer horizontalen Entfernung von 20 Metern erreicht. }} | ||
| + | d) | ||
| + | {{Lösung versteckt mit Rand| | ||
| + | Scheitelpunkt einsetzen:<br /> | ||
| + | <math>f(x)=a(x-10)^2+120</math> <br> | ||
| + | Schnittpunkt mit der y-Achse <math>P(0\mid18)</math> einsetzen, nach a auflösen:<br> | ||
| + | <math> | ||
| + | \begin{array}{rlll} | ||
| + | f(0)&=&18 \\ | ||
| + | a(0-10)^2+120&=&18 \\ | ||
| + | 100a+120&=&18 &\mid -120 \\ | ||
| + | a&=&-1.02 | ||
| + | \end{array} | ||
| + | </math><br /> | ||
| + | a einsetzen:<br /> | ||
| + | <math>\Rightarrow f(x)=-1.02(x-10)^2+120</math> | ||
| + | }} | ||
| + | Zusatzaufgabe: | ||
| + | {{Lösung versteckt mit Rand| | ||
| + | Wir müssen also den x-Wert zum zugehörigen <math>f(x)=30</math> berechnen. <br> | ||
| + | <math>30=-0.2x^2+8x+18 \mid -30 </math> <br /> | ||
| + | <math>\Leftrightarrow 0=-0.2x^2+8x-12 </math><br /> | ||
| − | |||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
| − | 0 & = & -0 | + | 0 & = & -0.2x^2+8x-12 & \mid :(-0.2) \\ |
| − | + | &=& x^2-40x+60 | |
| − | + | ||
| − | + | ||
| − | + | ||
\end{array} | \end{array} | ||
| − | </math><br> | + | </math><br /> |
| + | <math> \Rightarrow p=-40, q=60</math> <br> | ||
| + | |||
<math> | <math> | ||
| − | \Rightarrow x_1= | + | \begin{array}{rll} |
| − | </math><br> | + | x_{1/2} &=& -\frac{-40}{2} \pm \sqrt{{\left ( \frac{-40}{2} \right )}^2 -60} \\ |
| − | + | &=& 20 \pm 18.44 \\ | |
| − | </popup> | + | \end{array} |
| + | </math><br> | ||
| + | |||
| + | <math> | ||
| + | \Rightarrow x_1=18.44+20=38.44 </math> und <math> x_2=-18.44+20=1.56</math><br /> | ||
| + | Die Rakete hat also theoretisch nach ca. 1.56 Metern und nach ca. 38.44 Metern eine Flughöhe von 30 Metern. | ||
| + | }} | ||
| + | |||
| + | </popup>}} | ||
| + | |||
| + | [[Kategorie:Digitale Werkzeuge in der Schule|!]] | ||
Aktuelle Version vom 28. Dezember 2018, 00:04 Uhr
|
In diesem Lernpfad geht es darum, dass du im Bereich der quadratischen Funktionen noch etwas sicherer wirst. Im Laufe dieses Lernpfads kannst du also noch einmal die Scheitelpunktform und die Normalform der quadratischen Funktion wiederholen und einige Übungsaufgaben dazu erledigen. Am Ende dieses Lernpfads erwartet dich dann noch eine Anwendungsaufgabe zu diesem Themengebiet. |
Inhaltsverzeichnis |
Die Scheitelpunktform
Die Parameter der Scheitelpunktform
|
Fülle den folgenden Lückentext aus.
|
Scheitelpunktformen und ihre Graphen
|
Ordne den angegebenen Graphen ihre Scheitelpunktform zu, indem du die zusammengehörigen Felder aufeinander ziehst. |
|
Skizziere die angegebenen Funktionen als Graphen in dein Heft:
|
Funktionsgleichungen aufstellen
|
Stelle mit Hilfe der angegebenen Punkte die Funktionsgleichung auf: a) Wir suchen die Parabel f mit dem Scheitelpunkt S(-3I1), die durch den Punkt P(2I6) verläuft. b) Gesucht ist die Parabel g, die die y-Achse bei -4 schneidet, und die ihren Scheitelpunkt bei S(1I-1) hat. |
Scheitelpunktform und Normalform
|
Fülle den Lückentext aus, indem du in die Lücken klickst und die richtige Antwort auswählst. |
Von der Scheitelpunktform zur Normalform
|
Forme die folgenden Scheitelpunktformen in deinem Heft in die Normalenformen um und klicke dann das richtige Ergebnis an. |
Von der Normalform zur Scheitelpunktform
In Aufgabe 5 hast du wiederholt, wie man die Normalform in die Scheitelpunktform überführt. Das kannst du in Aufgabe 9 üben. Zuerst wollen wir uns aber noch einmal genau ansehen, was die quadratische Ergänzung ist und warum man sie für die Umwandlung braucht. Wenn du dich mit der quadratischen Ergänzung schon sicher fühlst, kannst du direkt Aufgabe 9 bearbeiten.
Die quadratische Ergänzung ist ein Trick, den man benutzt, wenn die man die 1. oder 2. binomische Formel rückwärts anwenden anwenden möchte.
Zur Erinnerung:
30px Merke
1. Binomische Formel:
|
Wir wollen jetzt also nicht die Klammer ausmultiplizieren, sondern den Term zu so einem Klammerausdruck umformen, z.B. den Term 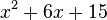 .
.
Wie das funktioniert, kannst du in dieser Aufgabe noch mal wiederholen:
|
Wichtig: Wenn for dem x2 ein Faktor steht, muss dieser zunächst ausgeklammert werden. |
|
Ergänze in dem folgenden Beispiel die Umformungsschritte, indem du sie an die richtige Stelle ziehst. |
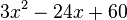 | Faktor 3 ausklammern
| Faktor 3 ausklammern
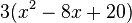 | Faktor 2 "herausziehen"
| Faktor 2 "herausziehen"
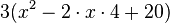 | quadratische Ergänzung
| quadratische Ergänzung
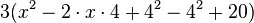 | 2. Binomische Formel
| 2. Binomische Formel
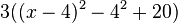 | zusammenfassen
| zusammenfassen
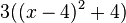 | ausmultiplizieren
| ausmultiplizieren
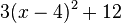
|
|
Anwendungsaufgabe "Rakete"
|
Zum Abschluss eines Volksfestes wird ein Feuerwerk vom Dach eines Parkhauses abgeschossen. Der Pyrotechniker hat für die Beschreibung der Flugbahn einer Rakete die Funktion a) Berechne b) Berechne, wie weit die Rakete fliegen würde, bis sie auf den Boden auftrifft. c) Nach wieviel Metern erreicht die Rakete ihre maximale Höhe? Welche Höhe erreicht sie? d) Bei gleichbleibendem Startpunkt soll die Flugbahn so verändert werden, dass nach 10 m Entfernung vom Startpunkt die maximale Höhe von 120 m erreicht wird. Bestimme eine Funktionsgleichung für diese neue Flugbahn. Zusatzaufgabe* Berechne die horizontale Entfernung vom Startpunkt, in der die Rakete theoretisch eine Flughöhe von 30 m hat. |
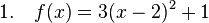
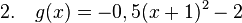

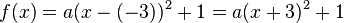
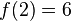
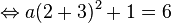
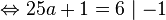
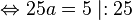
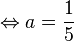
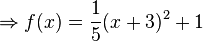
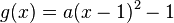
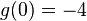
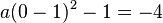
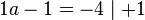
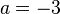
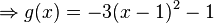
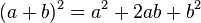
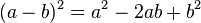
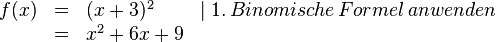
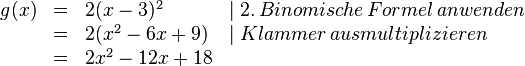
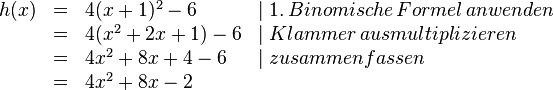
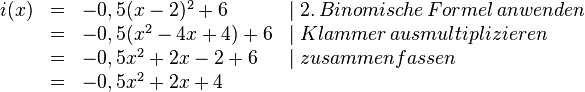
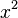 zunächst auszuklammern!
zunächst auszuklammern!
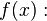
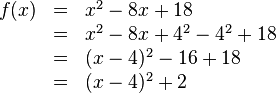
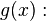
![\begin{array}{rll}
g(x)&=&5x^2+30x+43 \\ &=&5(x^2+6x+8.6) \\ &=&5(x^2+6x+3^2-3^2+8.6) \\ &=&5[(x+3)^2-3^2+8.6] \\ &=&5[(x+3)^2-0.4] \\ &=&5(x+3)^2-2
\end{array}](/images/math/f/4/c/f4c416dfb6dcdbadc261c78110aa4cf8.png)
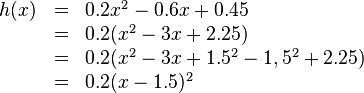
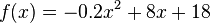
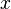 der horizontalen Entfernung von der Abschussstelle und
der horizontalen Entfernung von der Abschussstelle und 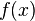 der Höhe der Rakete; jeweils in Meter.
der Höhe der Rakete; jeweils in Meter.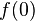 und beschreibe, was dieser Wert im Anwendungskontext bedeutet.
und beschreibe, was dieser Wert im Anwendungskontext bedeutet.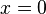 ist?
ist? 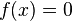 und berechne die Nullstellen mithilfe der p-q-Formel.
und berechne die Nullstellen mithilfe der p-q-Formel. 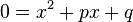 liefert die p-q-Formel die Lösungen
liefert die p-q-Formel die Lösungen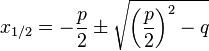 .
.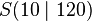 und des Punktes
und des Punktes 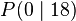 auf.
auf.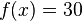 ist.
ist. 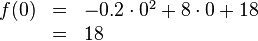
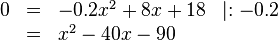
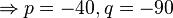
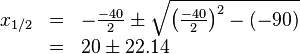
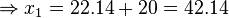 und
und 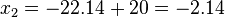
![\begin{array}{rlll}
f(x) & = & -0.2x^2+8x+18 &\mid -0.2 \, vorklammern \\
&=& -0.2(x^2-40x-90) &\mid quadratische \, Erg\ddot{a} nzung +20^2-20^2 \\
&=& -0.2(x^2-2 \cdot 20x+20^2-20^2-90) & \mid 2. Binomische \, Formel \\
&=& -0.2[(x-20)^2-490] & \mid ausmultiplizieren \\
&=& -0.2 (x-20)^2+98
\end{array}](/images/math/2/e/a/2eace7293d7607a476cdbe9be4dd8624.png)
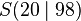 , die maximale Höhe von 98 Metern wird also bei einer horizontalen Entfernung von 20 Metern erreicht.
, die maximale Höhe von 98 Metern wird also bei einer horizontalen Entfernung von 20 Metern erreicht. 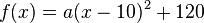
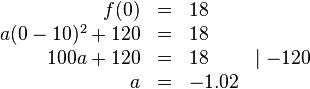
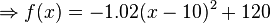
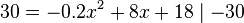
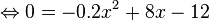
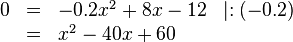
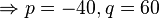
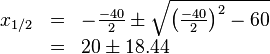
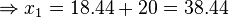 und
und