Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Testseite: Unterschied zwischen den Versionen
| (40 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | |||
| + | <div style="margin:0; margin-right:3px; margin-left:3px; border:3px solid #FF7F00; padding: 1em 1em 1em 1em; background-color:#C6E2FF; align:left;"> <center><table border="0" width="750px" cellpadding=5 cellspacing=15> <tr><td width="300px" valign="top"> | ||
| + | Auf dieser Seite findest du Aufgaben, die dein Verständnis zum '''Sachkontext von Ableitungen''' vertiefen. Du wiederholst, Ergebnisse im Sachzusammenhang zu interpretieren, Signalwörter in den Aufgabenstellungen zu erkennen und diese mit den entsprechenden rechnerischen Vorgehensweisen zu verknüpfen. Außerdem vertiefst du an verschiedenen Beispielen den Zusammenhang zwischen der Funktion und den einzelnen Ableitungen. Dies tust du vor allem mit Bezug auf die Einheiten der Funktionswerte. | ||
| + | Die Aufgaben 1-3 dienen als Einstieg und sind leichter zu lösen. In den Aufgaben 4-5 kannst du schwierigere Probleme lösen. Falls du dich schon sehr sicher fühlst, kannst du dich an die letzte Aufgabe begeben. | ||
| + | </td></tr></table></center> </div> | ||
| + | ==Aufgabe 1: Dieselpreise== | ||
| + | {{Aufgaben|1: Dieselpreise|Die Abbildung 1.1 zeigt die Entwicklung des Dieselpreises in Deutschland im Zeitraum vom 12.10.2018 bis zum 18.10.2018. <br /> <br /> | ||
| + | [[Datei:Dieselpreis DiWerS.png|thumb|Abb. 1.1: Dieselpreisentwicklung|1000px|zentriert]]<br /> | ||
| + | |||
| + | '''a)''' Berechnen den durchschnittlichen Preisanstieg im Zeitraum vom 13.10.2018 bis zum 16.10.2018.<br /> | ||
| + | Hier kannst du deine Lösung eintragen und schauen, ob sie richtig ist. | ||
| + | <iframe src="https://learningapps.org/watch?v=pu9cnvh9t18" style="border:0px;width:100%;height:200px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <br /> | ||
| + | <popup name="Tipp"> Gesucht ist die durchschnittliche Änderungsrate, wobei f(5) den Dieselpreis am 17.10.2018 angibt, d.h. da der 17.10.2018 der fünfte Tag ist, betrachten wir x=5.</popup> | ||
| + | <popup name="Lösung"> 0 €/Tag </popup><br /> | ||
| + | <br /> | ||
| + | '''b)''' Beurteile die Aussagekraft des in Teil a) ermittelten Durchschnittswertes und notiere dein Ergebnis im Heft.<br /> | ||
| + | <popup name="Tipp"> Wie teuer war der Diesel am 14.10.2018, wenn man nur den Durchschnittswert betrachtet. </popup> | ||
| + | <popup name="Lösung"> Betrachtet man den durchschnittlichen Preisanstieg im Bereich vom 13.10.2018 bis zum 16.10.2018, so entsteht der Eindruck, dass sich der Dieselpreis in diesem kompletten Zeitraum nicht geändert hat. Es wäre somit egal gewesen, wann man in diesem Zeitraum tankt. Betrachtet man allerdings die Abbildung 1.1, so wird deutlich, dass dies nicht der Fall ist. </popup><br /> | ||
| + | |||
| + | <br /> }} | ||
| + | ==Aufgabe 2: Zuordnen== | ||
| + | {{Aufgaben|2: Zuordnen|Der Graph der Funktion f(t) beschreibt die Flugbahn eines Balls. f(t) gibt die Höhe in Metern in Abhängigkeit von der Zeit in Sekunden an. <br /> | ||
| + | Fülle den folgenden Lückentext aus: | ||
| + | <iframe src="https://learningapps.org/watch?v=pxert0c0t18" style="border:0px;width:100%;height:700px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <popup name= "Tipp 1" >Die Geschwindigkeit des Balls in einem Punkt s ist gerade die Steigung in diesem Punkt.</popup> | ||
| + | <popup name= "Tipp 2" >In welchem Zusammenhang stehen Höhe des Balls, die Geschwindigkeit und die Beschleunigung in Bezug auf ihre Ableitung? </popup> | ||
| + | <popup name= "Tipp 3" >Wenn die Funktion an der Stelle s die stärkste Steigung hat, dann bedeutet dies für die 1. Ableitung, dass sie an der Stelle s einen Hochpunkt hat. Was bedeutet das für die 2.Ableitung ?</popup> | ||
| + | <popup name= "Tipp 4" >Was beschreibt die Funktion f(t)? Wie sieht der Graph ungefähr aus? Welche Steigung ist in diesem Punkt s vorzufinden? Was bedeutet dies für den Wert f'(s)?</popup> | ||
| + | <popup name= "Tipp 5" >Wie hoch ist der Ball, wenn er auf der Erdoberfläche auftrifft?</popup> | ||
| + | <popup name= "Tipp 6" >Zu welchem Zeitpunkt wurde der Ball abgworfen?</popup> | ||
| + | <popup name= "Tipp 7" >Um die durchschnittliche Geschwindigkeit zu bestimmen, betrachte ich die Änderung der Höhe für den Anfangs- und Endwert des Bereiches.</popup> | ||
| + | <popup name= "Lösung" >Wenn die Geschwindigkeit des Balls zu einem Zeitpunkt s gesucht ist, bedeutet dies, dass ich die momentane Änderungsrate der Funktion f(t) an der Stelle s bestimmen muss. Dazu berechne ich f '(s). | ||
| + | |||
| + | Möchte ich allerdings die Beschleunigung des Balls zu einem Zeitpunkt s betrachten, so suche ich die momentane Änderungsrate der Ableitung der Funktion f(t) an der Stelle s. Dazu berechne ich f ''(s). | ||
| + | |||
| + | Wird nach der stärksten Steigung der Funktion f(t) gefragt, so muss ich die Wendestelle bestimmen. Dafür muss f ''(s)=0 und f '''(s) ≠ 0 gelten. | ||
| + | |||
| + | Soll ich die maximale Höhe des Balls angeben, so muss ich den Hochpunkt bestimmen. Dafür muss f '(s)=0 und f ''(s) < 0 gelten. | ||
| + | |||
| + | Wann der Ball wieder auf der Erdoberfläche aufkommt, gibt die Nullstelle an. Dazu berechne ich f(s)=0. | ||
| + | |||
| + | Außerdem gibt der y-Achsenabschnitt an, aus welcher Höhe der Ball abgeworfen wurde. Hierzu berechne ich f(0). | ||
| + | |||
| + | Suche ich die durchschnittliche Geschwindigkeit in einem Bereich m bis n, so suche ich für diesen Bereich die durchschnittliche Änderungsrate, dies ist gerade der Wert des Differentenquotienten.</popup>}} | ||
| + | ==Aufgabe 3: Silvesterkracher== | ||
| + | |||
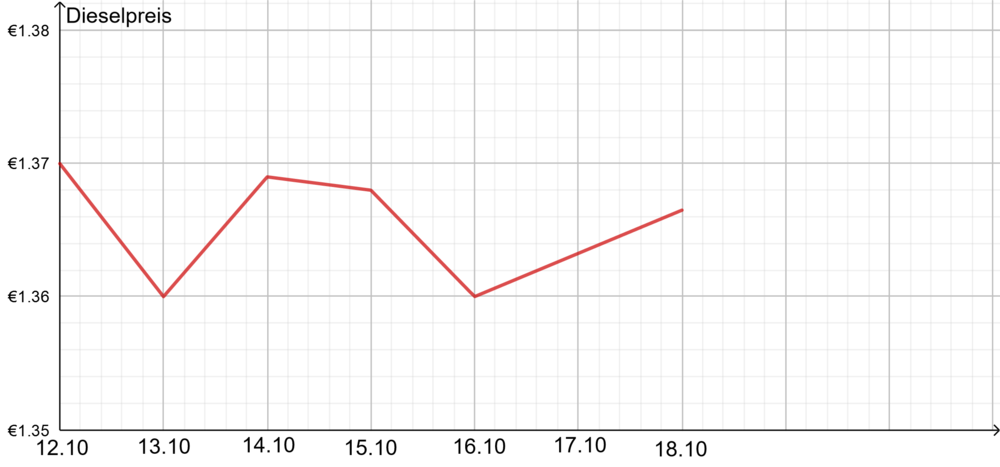
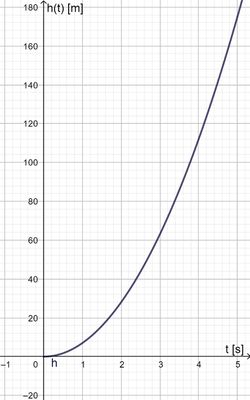
| + | {{Aufgaben|3: Silvesterkracher|[[Datei:Rakete.jpg|Abb. 3.1: Höhe einer Feuerwerksrakete |thumb|250px|rechts]]Die Höhe einer gezündeten Feuerwerksrakete kann in den ersten fünf Sekunden nach dem Start annähernd durch die Funktion <math>h(t)=7t^2</math> beschrieben werden (siehe Abbildung 3.1). Dabei wird die Zeit t nach dem Start in Sekunden und die Höhe h(t) in Metern angegeben. <br/> | ||
| + | '''a)''' Bestimme die folgenden Werte. <br/> | ||
| + | # <math>h(2)</math> | ||
| + | # <math>h(4)-h(1)</math> | ||
| + | # <math>\frac{h(4)-h(1)}{4-1}</math> | ||
| + | # <math>h'(3)</math> | ||
| + | # <math>\frac{h(t)-h(4,5)}{t-4,5}</math> für t → 4,5 | ||
| + | # <math>h'(4,5)</math> | ||
| + | |||
| + | <iframe src="https://learningapps.org/watch?v=pk702c34c18" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <popup name="Tipp"> | ||
| + | Setze die entsprechenden Werte für t in die entsprechende Funktion ein. Die Ableitung der Funktion ist h'(t)=14t. Für 5. überlege, was dieser Ausdruck ist und ob du diesen anders schreiben kannst. | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | '''b)''' Interpretiere alle Ergebnisse aus a) im Sachzusammenhang. Schreibe in dein Heft. <br/> | ||
| + | <popup name="Lösung"> | ||
| + | # Die Rakete hat nach zwei Sekunden eine Höhe von 28 Metern. | ||
| + | # Zwischen der ersten und der vierten Sekunde überwindet die Rakete eine Höhe von 105 Metern. | ||
| + | # Zwischen der ersten und der vierten Sekunde beträgt die durchschnittliche Geschwindigkeit der Rakete 35 m/s. | ||
| + | # Drei Sekunden nach dem Start ist die momentane Geschwindigkeit der Rakete 42 m/s. | ||
| + | # 4,5 Sekunden nach dem Start der Rakete beträgt die Geschwindigkeit der Rakete 63 m/s. | ||
| + | # siehe 5. | ||
| + | </popup> | ||
| + | '''c)''' Wie groß ist die Beschleunigung des Feuerwerkskörpers drei Sekunden nach dem Start?<br/> | ||
| + | <iframe src="https://learningapps.org/watch?v=paog8ud6a18" style="border:0px;width:100%;height:150px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | '''d)''' Erkläre, warum die vorliegende Modellierung nur in den ersten fünf Sekunden nach dem Start geeignet ist? Schreibe in dein Heft. | ||
| + | <popup name="Tipp"> | ||
| + | Überlege, wie der Graph der Funktion für Werte von t>5 verläuft. | ||
| + | </popup> | ||
| + | <popup name="Lösung"> | ||
| + | Die Rakete kann nicht unendlich hoch fliegen und bereits nach 5 Sekunden ist eine Höhe von 175 Metern erreicht. Nach der Explosion des Feuerwerkskörpers fällt er wieder runter und verliert somit an Höhe, die Steigung der Funktion müsste demnach irgendwann wieder negativ werden, was nach der obigen Modellierung für keine positiven Werte von t eintrifft. | ||
| + | </popup> | ||
| + | }} | ||
| + | |||
| + | |||
| + | ==Aufgabe 4: Aussagen der Ableitungsfunktion und Änderung der Einheiten== | ||
| + | {{Aufgaben|4: Aussagen der Ableitungsfunktion und Änderung der Einheiten| | ||
| + | |||
| + | '''a)''' Eine Funktion f(t) beschreibt die zurückgelegte Strecke eines Fahrradfahrers in Metern in Abhängigkeit von der Zeit t in Sekunden. Vervollständige die folgenden Aussagen. | ||
| + | <iframe src="https://learningapps.org/watch?v=ps4fbw3jt18" style="border:0px;width:100%;height:250px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | '''b)''' In einem Wald werden nach einer Rodung neue Bäume gepflanzt. Der Förster misst die durchschnittliche Höhe der Bäume in Metern monatlich aus, notiert seine Messwerte und modelliert den Sachverhalt in einer Funktion f(x). Vervollständige die folgenden Aussagen. | ||
| + | <iframe src="https://learningapps.org/watch?v=p57tu5mda18" style="border:0px;width:100%;height:250px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <popup name="Tipp zu a) und b)"> | ||
| + | Bei a) ist die Einheit der Funktionswerte der Funktion f(t) Meter. Die Werte der x-Achse sind in der Einheit Sekunden gegeben. Wenn man die Ableitung bildet, verändert sich die Einheit der Funktionswerte! Man dividiert die Einheit der y-Achse durch die Einheit der x-Achse. Bei a) erhält man für die Funktionswerte der Ableitungsfunktion also die Einheit m/s. Dies steht für eine Geschwindigkeit. Gehe in anderen Beispielen genauso vor. | ||
| + | </popup> | ||
| + | |||
| + | '''c)''' Zum Herbst wird das Wasser im städtischen Freibad aus dem Becken abgelassen. Eine Funktion f(x) ist die Ableitungsfunktion von g(x) und beschreibt die Abflussrate in Kubikmetern pro Stunde, wobei x die Zeit in Stunden angibt. Vervollständige die folgende Aussage. | ||
| + | <iframe src="https://learningapps.org/watch?v=pp7vnup6518" style="border:0px;width:100%;height:200px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | |||
| + | <popup name="Tipp zu c)"> | ||
| + | Versuche hier andersherum zu denken und überlege, wie du die Einheit und somit den Sachverhalt der ursprünglichen Funktionswerte ermitteln kannst, wenn du diese Informationen zu der Ableitungsfunktion gegeben hast. | ||
| + | </popup><br /> | ||
| + | |||
| + | }} | ||
| + | |||
| + | ==Aufgabe 5: Ein Tag im Zoo== | ||
| + | |||
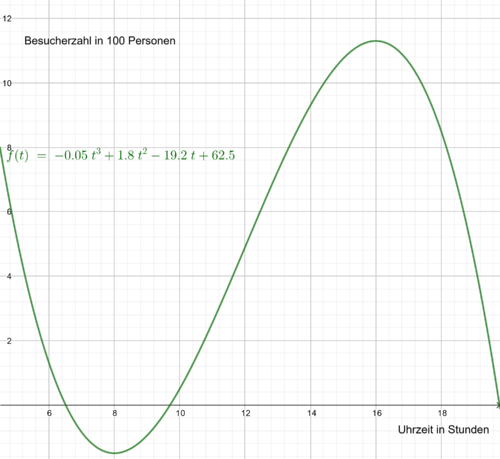
| + | {{Aufgaben|5 : Ein Tag im Zoo}}Ein Zoo ist bekanntermaßen in den Sommerferien am besten besucht. Die Besucherzahlen eines bestimmten Zoos (in 100 Personen) kann durch die Funktion <br /> b(t) = - 0,05 t³ + 1,8 t² - 19,2 t + 62,5 für 10 < t ≤ 19,5 <br /> näherungsweise beschrieben werden. Dabei gibt ''t'' die Uhrzeit in Stunden an.<br /> <br /> | ||
| + | [[Datei:Besucherzahlen2.png|500px|zentriert|thumb|Abb. 5.1: Besucherzahl eines Zoos]] <br /> | ||
| + | Rechne die folgenden Aufgaben im Heft und vergleiche mit den angegebenen Lösungsvorschlägen. <br /> | ||
| + | '''a)''' Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?<br/> | ||
| + | <popup name="Tipp">Die Ableitung lautet: b´(t) = - 0,15 t² + 3,6 t - 19,2 </popup> | ||
| + | <popup name="Lösung">Die Nullstellen der Ableitung entsprechen den Maximalstellen der Normalfunktion. Setzt man die Ableitung gleich 0, also 0 = b´(t) = - 0,15 t² + 3,6 t - 19,2 , dann erhält man <math>t_1</math> = 8 und <math>t_2</math> = 16. Da der Zoo erst um 10:00 Uhr (also t = 10) öffnet, ist <math>t_2</math> die einzige Lösung. <br/> Setzt man das in die Funktion ein erhält man: b(16) = 11,3 . <br/>'''Die Antwort: Mit 1130 Besuchern sind um 16:00 Uhr die meisten Menschen im Zoo.</popup> | ||
| + | <br/> | ||
| + | '''b)''' Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen? <br/> | ||
| + | <popup name="Tipp">Bei dieser Aufgabe ist es wichtig, sich den Definitionsbereich noch einmal genauer anzugucken. Du darfst auch mit der Abbildung 5.1 deine Begründung unterstützen.</popup> | ||
| + | <popup name="Lösung">Die Besucherzahl ist um 19:30 Uhr am geringsten. Das ist der einzige Nullpunkt im Definitionsbereich. Die Minimalstelle liegt, wie man in der Abbildung deutlich erkennen kann unterhalb der x-Achse und eine negative Besucherzahl ist nicht möglich. Außerdem liegt diese Stelle nicht mehr im Definitionsbereich.</popup> | ||
| + | <br/> | ||
| + | '''c)''' Zu welcher Uhrzeit ist der Andrang in den Zoo am größten? <br/> | ||
| + | <popup name="Tipp 1">Mit der Frage nach dem größten Andrang ist der größte Zuwachs an Besuchern gemeint.</popup> | ||
| + | <popup name="Tipp 2">Die zweite Ableitung lautet: b´´(t) = - 0,3 t + 3,6</popup> | ||
| + | <popup name="Lösung">Indem die zweite Ableitung gleich 0 gesetzt wird, kann man die Wendestelle ausrechnen. Daraus ergibt sich t = 12. Also sind die meisten Menschen um 12:00 Uhr auf den Weg in den Zoo.</popup>}} | ||
| + | |||
| + | ==Aufgabe 6: Die Autofahrt== | ||
| + | {{Aufgaben| 6 : Die Autofahrt|Familie Müller fährt zusammen in den Urlaub. Der Sohn Peter möchte gerne wissen, wie weit sie insgesamt gefahren sind. Dazu hat er die Geschwindigkeit des Autos zu bestimmten Zeitpunkten auf der Anzeige im Auto abgelesen und sich notiert. Die Geschwindigkeit könnte man in einem Graphen darstellen, wie in Abbildung 6.1. <br/> | ||
| + | [[Datei:Geschwindigkeitsnotizen1.png|1000px|zentriert|thumb|Abb. 6.1: Geschwindigkeitsprofil einer Urlaubsfahrt]]<br /> | ||
| + | |||
| + | '''a)''' Fülle die Lücken mit den richtigen Antworten.<br /> | ||
| + | <iframe src="https://learningapps.org/watch?v=phzt4r2ba18" style="border:0px;width:100%;height:300px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <popup name="Tipp">Auf den einzelnen Straßen gelten folgende Geschwindigkeitsbeschränkungen: <br/> verkehrsberuhigte Straße: 5 km/h <br/> Straße der "30-Zone": 30 km/h <br/> Straße innerorts: 50 km/h <br/> Landstraße: 100 km/h <br/> Autobahn: 130 km/h </popup> | ||
| + | |||
| + | |||
| + | |||
| + | '''b)''' Was passiert in den Zeiträumen, in denen die Geschwindigkeit nicht konstant sind? <br /> | ||
| + | <popup name="Lösung">Wenn der Graph fällt, sinkt somit die Geschwindigkeit. Also wird das Auto gebremst. <br/> Steigt der Graph, so steigt auch die Geschwindigkeit und der Fahrer beschleunigt.</popup> <br /> | ||
| + | |||
| + | '''c)''' Wie viele Kilometer ist das Auto von Peters Familie in dem Zeitraum von Minute 67 bis Minute 82 gefahren? | ||
| + | |||
| + | Schreibe die Lösung in dein Heft. <br /> | ||
| + | <popup name="Tipp 1">Beachte die Einheiten. Die Fahrtzeit ist in Minuten [min] angegeben und die Geschwindigkeit in Stundenkilometer/Kilometer pro Stunde [km/h].</popup> | ||
| + | <popup name="Tipp 2">Wie lang ist die Zeit zwischen Minute 67 bis Minute 82? Rechne diese Differenz von Minuten [min] in Stunden [h] um.</popup> | ||
| + | <popup name="Tipp 3">In dem Zeitraum liegen 15 Minuten, die entsprechen 1/4 Stunde. Wenn man 15 Minuten, also eine Viertelstunde, mit einer Geschwindigkeit von 50 km/h fährt. Wie viel Strecke hat man dann zurückgelegt?</popup> | ||
| + | <popup name="Lösung">Von Minute 67 bis Minute 82 ist eine Viertelstunde vergangen, in der die Familie 12,5 km zurückgelegt hat.</popup> <br /> | ||
| + | |||
| + | '''d)''' Wie viele Kilometer hat Peters Familie in den ersten 2 Stunden näherungsweise zurückgelegt? | ||
| + | |||
| + | "Näherungsweise" bedeutet an dieser Stelle musst du nur die Phasen konstanter Geschwindigkeit in Betracht ziehen. Schreibe die Lösung in dein Heft.<br /> | ||
| + | <popup name="Tipp">Wenn man die Beschleunigs- und Bremsphasen beiseite lässt, erhählt man fünf einzelne Abschnitte, die man wie in Aufgabe '''c)''' berechnen kann. (Zeit*Geschwindigkeit=Strecke)</popup> | ||
| + | <popup name="Lösung"> Strecke AB (6 Minuten): 0,1 h * 30 km/h = 3 km <br/> Strecke CD (20 Minuten): 0,333 h * 50 km/h = 16,666 km <br/> Strecke EF (30 Minuten): 0,5 h * 100 km/h = 50 km <br/> Strecke GH (15 Minuten): 0,25 h * 50 km/h = 12,5 km (siehe '''c)''') <br/> Strecke IJ (35 Minuten): 0,583 h * 100 km/h = 58,33 km <br/> '''Insgesamt also:''' 3 km + 16,66 km + 50 km + 12,5 km + 58,33 km = 140,5 (Rundungsfehler sind hier möglich!)</popup> | ||
| + | <br /> | ||
| + | '''e)''' Wir nehmen an, der abgebildete Graph beschreibt die Ableitung einer Funktion. Was gibt dann die Funktion an und wovon ist sie abhängig? | ||
| + | |||
| + | Schreibe die Lösung in dein Heft.<br /> | ||
| + | <popup name="Tipp">Betrachte die vorherigen Aufgaben und ihre Ergebnisse noch einmal.</popup> | ||
| + | <popup name="Lösung">Wenn die Ableitung die Geschwindigkeit in Abhängigkeit von der Zeit angibt, dann gibt die Funktion die Strecke in Abhängigkeit von der Zeit an.</popup> <br /> | ||
| + | |||
| + | '''f)''' Berechne die durchschnittliche Geschwindigkeit, die Peters Familie in den ersten zwei Stunden gefahren ist.<br /> | ||
| + | <popup name="Lösung">Die durchschnittliche Geschwindigkeit ergibt sich durch die gefahrene Strecke dividiert durch die Zeitspanne (2h). Aus Aufgabenteil '''d)''' kennen wir die gefahrene Strecke näherungsweise: | ||
| + | <br/>Also: '''140,5 km / 2 h = 70,25 km/h''' | ||
| + | <br/>''Auch hier kann dein Ergebnis abweichen, wenn du in '''d)''' ein anderes Ergebnis berechnet hast''</popup>}} | ||
| + | |||
| + | |||
| + | |||
==Spielwiese== | ==Spielwiese== | ||
| − | ===Schreiben im Wiki | + | ===Schreiben im Wiki== |
Neben normalem Text kann man auch ''kursiven'' oder '''fett gedruckten Text''' schreiben. <span style="color:red">Ebenso sind andere Farben möglich, um etwas hervorzuheben.</span> | Neben normalem Text kann man auch ''kursiven'' oder '''fett gedruckten Text''' schreiben. <span style="color:red">Ebenso sind andere Farben möglich, um etwas hervorzuheben.</span> | ||
<popup name="Versteckte Hinweise und Lösungen">Ganz einfach per Mausklick aktivierbar</popup> | <popup name="Versteckte Hinweise und Lösungen">Ganz einfach per Mausklick aktivierbar</popup> | ||
===Vorlagen=== | ===Vorlagen=== | ||
{{Aufgabe|Tangente}} | {{Aufgabe|Tangente}} | ||
| − | {{ | + | {{Aufgaben|1|Sachzusammenhang}} |
{{Aufgaben|Der Parameter a|Änderung}} | {{Aufgaben|Der Parameter a|Änderung}} | ||
{{Übung|Ableitungsregeln}} | {{Übung|Ableitungsregeln}} | ||
Aktuelle Version vom 28. Oktober 2018, 16:55 Uhr
|
Auf dieser Seite findest du Aufgaben, die dein Verständnis zum Sachkontext von Ableitungen vertiefen. Du wiederholst, Ergebnisse im Sachzusammenhang zu interpretieren, Signalwörter in den Aufgabenstellungen zu erkennen und diese mit den entsprechenden rechnerischen Vorgehensweisen zu verknüpfen. Außerdem vertiefst du an verschiedenen Beispielen den Zusammenhang zwischen der Funktion und den einzelnen Ableitungen. Dies tust du vor allem mit Bezug auf die Einheiten der Funktionswerte. Die Aufgaben 1-3 dienen als Einstieg und sind leichter zu lösen. In den Aufgaben 4-5 kannst du schwierigere Probleme lösen. Falls du dich schon sehr sicher fühlst, kannst du dich an die letzte Aufgabe begeben. |
Inhaltsverzeichnis |
Aufgabe 1: Dieselpreise
|
Die Abbildung 1.1 zeigt die Entwicklung des Dieselpreises in Deutschland im Zeitraum vom 12.10.2018 bis zum 18.10.2018. a) Berechnen den durchschnittlichen Preisanstieg im Zeitraum vom 13.10.2018 bis zum 16.10.2018.
|
Aufgabe 2: Zuordnen
|
Der Graph der Funktion f(t) beschreibt die Flugbahn eines Balls. f(t) gibt die Höhe in Metern in Abhängigkeit von der Zeit in Sekunden an. |
Aufgabe 3: Silvesterkracher
Die Höhe einer gezündeten Feuerwerksrakete kann in den ersten fünf Sekunden nach dem Start annähernd durch die Funktion 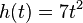 beschrieben werden (siehe Abbildung 3.1). Dabei wird die Zeit t nach dem Start in Sekunden und die Höhe h(t) in Metern angegeben. beschrieben werden (siehe Abbildung 3.1). Dabei wird die Zeit t nach dem Start in Sekunden und die Höhe h(t) in Metern angegeben. a) Bestimme die folgenden Werte.
c) Wie groß ist die Beschleunigung des Feuerwerkskörpers drei Sekunden nach dem Start? |
Aufgabe 4: Aussagen der Ableitungsfunktion und Änderung der Einheiten
|
b) In einem Wald werden nach einer Rodung neue Bäume gepflanzt. Der Förster misst die durchschnittliche Höhe der Bäume in Metern monatlich aus, notiert seine Messwerte und modelliert den Sachverhalt in einer Funktion f(x). Vervollständige die folgenden Aussagen. c) Zum Herbst wird das Wasser im städtischen Freibad aus dem Becken abgelassen. Eine Funktion f(x) ist die Ableitungsfunktion von g(x) und beschreibt die Abflussrate in Kubikmetern pro Stunde, wobei x die Zeit in Stunden angibt. Vervollständige die folgende Aussage.
|
Aufgabe 5: Ein Tag im Zoo
|
{{{2}}} |
b(t) = - 0,05 t³ + 1,8 t² - 19,2 t + 62,5 für 10 < t ≤ 19,5
näherungsweise beschrieben werden. Dabei gibt t die Uhrzeit in Stunden an.
Rechne die folgenden Aufgaben im Heft und vergleiche mit den angegebenen Lösungsvorschlägen.
a) Zu welcher Uhrzeit befinden sich am meisten Besucher in dem Zoo? Und wie viele sind es?
b) Wann ist die Besucherzahl am geringsten? Und warum ist es falsch, an dieser Stelle nach der Minimalstelle zu suchen?
c) Zu welcher Uhrzeit ist der Andrang in den Zoo am größten?
Aufgabe 6: Die Autofahrt
|
Familie Müller fährt zusammen in den Urlaub. Der Sohn Peter möchte gerne wissen, wie weit sie insgesamt gefahren sind. Dazu hat er die Geschwindigkeit des Autos zu bestimmten Zeitpunkten auf der Anzeige im Auto abgelesen und sich notiert. Die Geschwindigkeit könnte man in einem Graphen darstellen, wie in Abbildung 6.1. a) Fülle die Lücken mit den richtigen Antworten.
b) Was passiert in den Zeiträumen, in denen die Geschwindigkeit nicht konstant sind? c) Wie viele Kilometer ist das Auto von Peters Familie in dem Zeitraum von Minute 67 bis Minute 82 gefahren? Schreibe die Lösung in dein Heft. d) Wie viele Kilometer hat Peters Familie in den ersten 2 Stunden näherungsweise zurückgelegt? "Näherungsweise" bedeutet an dieser Stelle musst du nur die Phasen konstanter Geschwindigkeit in Betracht ziehen. Schreibe die Lösung in dein Heft.
Schreibe die Lösung in dein Heft. f) Berechne die durchschnittliche Geschwindigkeit, die Peters Familie in den ersten zwei Stunden gefahren ist. |
Spielwiese
=Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso sind andere Farben möglich, um etwas hervorzuheben.
Vorlagen
|
Tangente |
|
Sachzusammenhang |
|
Änderung |
30px Übung
Ableitungsregeln |
30px Merke
Differenzenquotient |
Dateien
Interaktive Applets
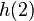
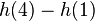
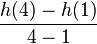
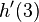
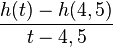 für t → 4,5
für t → 4,5
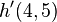
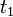 = 8 und
= 8 und 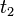 = 16. Da der Zoo erst um 10:00 Uhr (also t = 10) öffnet, ist
= 16. Da der Zoo erst um 10:00 Uhr (also t = 10) öffnet, ist