Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Die Steigung eines Funktionsgraphen in einem Punkt: Unterschied zwischen den Versionen
| (41 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| − | |||
</div> | </div> | ||
| Zeile 31: | Zeile 30: | ||
<iframe src="https://learningapps.org/watch?v=pmdztmg4j18" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pmdztmg4j18" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <popup name="Lösung">In der oberen Abbildung sind eine rote und eine blaue Gerade zu sehen, die den Graphen (hier in grün) berühren, bzw. schneiden. Bei der blauen Geraden handelt es sich um eine '''Tangente''' und bei der roten Gerade um eine '''Sekante'''. | ||
| + | Bewegt man die Punkte P und Q entlang der Kurve aufeinander zu, bis der Abstand zwischen ihnen minimal ist, so wird aus der '''Sekante''' | ||
| + | eine '''Tangente'''. | ||
| + | Betrachten wir den einzelnen Punkt P auf der Kurve, dann kann man fragen: "Wie groß ist '''die Steigung der Kurve an diesem Punkt'''?". | ||
| + | Man definiert: Die Steigung einer Kurve in einem Punkt P soll genau so groß sein, wie die Steigung '''einer Tangente''', welche die Kurve genau in diesem Punkt P berührt. | ||
| + | Die Steigung der Kurve in einem Punkt wird auch mit Hilfe ihrer '''ersten Ableitung'''in diesem Punkt beschrieben.</popup> | ||
| + | |||
}} | }} | ||
| + | |||
{{Aufgaben|2: Weiterführender Lückentext| | {{Aufgaben|2: Weiterführender Lückentext| | ||
| − | In diesem Applet siehst du den Graphen einer Funktion f und eine Gerade a. Weiterhin findest du in | + | In diesem Applet siehst du den Graphen einer Funktion f und eine Gerade a. Weiterhin findest du in diesem zwei Regler, an denen du x<sub>0</sub> und h einstellen kannst. |
| − | + | ||
Was fällt dir in Hinblick auf die Gerade a auf, wenn du den Regler von h verstellst? Fülle dazu den unter dem Applet stehenden Lückentext aus. | Was fällt dir in Hinblick auf die Gerade a auf, wenn du den Regler von h verstellst? Fülle dazu den unter dem Applet stehenden Lückentext aus. | ||
| − | <iframe scrolling="no" title="" src="https://www.geogebra.org/material/iframe/id/ | + | <iframe scrolling="no" title="Aufgabe 2" src="https://www.geogebra.org/material/iframe/id/euc92w5z/width/1536/height/658/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="900px" height="390px" style="border:0px;"> </iframe> |
| − | + | ''Hinweis: Beachte hier, dass die Dezimalzahlen mit Punkt und nicht wie gewohnt mit Komma geschrieben werden. Verwende für das Ausfüllen der Lücken bitte die folgende Schreibweise für Koordinaten: "(x/y)". '' | |
| − | + | <iframe src="https://learningapps.org/watch?v=pf5x5ysw218" style="border:0px;width:80%;height:350px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | |
| − | < | + | <popup name="Tipp zu Lücke 5">Sollte dir die 5. Lücke Probleme bereiten, überlege dir mithilfe des Applets, ob der Abstand zwischen den Punkten größer oder kleiner wird oder dieser gleich bleibt.</popup> |
| − | + | ||
| + | }} | ||
==Tangentengleichungen aufstellen== | ==Tangentengleichungen aufstellen== | ||
| − | {{Aufgaben|3 | + | |
| − | <iframe src="https://learningapps.org/watch?v= | + | {{Aufgaben|3|Die Tangente an die Funktion <math>f(x)=x^3+2x^2+5x-4</math> im Punkt <math>x=5</math> soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen. |
| + | <iframe src="https://learningapps.org/watch?v=ppge2zo5318" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | <popup name="Tipp">Eine Tangentengleichung hat die Form <math>y=mx+b</math>, wobei <math>m</math> die Steigung der Tangente ist und <math>b</math> der y-Achsenabschnitt.</popup> | ||
}} | }} | ||
| − | {{Aufgaben|4 | + | {{Aufgaben| 4| |
| − | + | ||
Bestimme die Gleichung der Tangente an die Funktion <math>f(x)=-1/3x^2+3</math> im Punkt <math>x=-3</math>. | Bestimme die Gleichung der Tangente an die Funktion <math>f(x)=-1/3x^2+3</math> im Punkt <math>x=-3</math>. | ||
| − | <popup name="Tipp"> | + | <popup name="Tipp">Erinnere dich zuerst daran, wie eine Tangentengleichung aussieht. Aufgabe 3 kann dir dabei helfen. |
| − | <popup name=" | + | Um die Steigung m zu ermitteln, benötigst du die Ableitung und musst anschließend die Ableitung im Punkt <math>x=-3</math> bestimmen. Was ist also der Zusammenhang zwischen der Ableitung in dem Punkt und der Steigung? |
| + | Wenn du die Steigung berechnet hast, fehlt dir nur noch der y-Achsenabschnitt. Dazu setzt du alle bekannten Werte in die allgemeine Tangentengleichung ein und formst um. | ||
| + | |||
| + | Schließlich kannst du die vollständige Tangentengleichung aufstellen. </popup> | ||
| + | <popup name="Lösungsschritt 1: Ableitung von f(x)">Die Ableitung von <math>f(x)</math> ist <math>f'(x)=-2/3x</math>.</popup> | ||
| + | <popup name="Lösungsschritt 2: Steigung im Punkt x=-3">Die Steigung im Punkt <math>x=-3</math> ist <math>f'(x)=-2/3x=2</math>.</popup> | ||
| + | <popup name="Lösungsschritt 3: y-Achsenabschnitt">Der y-Achsenabschnitt ist <math>0=2*(-3)+b</math>, also <math>b=6</math>.</popup> | ||
| + | <popup name="Lösungsschritt 4: Tangentengleichung">Die Gleichung der Tangente lautet <math>y=2x+6</math>.</popup> | ||
| + | |||
| + | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Aufgaben|5: Tangente durch Normale| | {{Aufgaben|5: Tangente durch Normale| | ||
| − | Berechne die Gleichung einer Tangente an die Funktion <math>f(x)=(x-1)^2+1</math> so, dass die Tangente g senkrecht zur Tangente a an der Stelle 1,25 (Punkt A) ist. | + | Berechne die Gleichung einer Tangente an die Funktion <math>f(x)=(x-1)^2+1</math> so, dass die Tangente g senkrecht zur Tangente a an der Stelle 1,25 (Punkt A) ist. Notiere deine einzelnen Rechenschritte in deinem Heft.<br /> |
| − | <iframe | + | |
| + | <iframe src="https://learningapps.org/watch?v=pqun2pnya18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | <popup name="Tipp 1">Berechne zunächst die Steigung der Tangente an Punkt A und nutze Tipp 2, falls du einen weiteren Hinweis benötigst.</popup> | ||
| + | <popup name="Tipp 2">Falls <math>m_1 \cdot m_2 = -1</math> gilt, so stehen die Geraden senkrecht aufeinander. (Mit <math>m_1, m_2</math> sind die beiden Steigungen der Geraden gemeint.)</popup> | ||
| + | <popup name="Lösung"> | ||
| + | 1. Schritt: <math>f(x)</math> ableiten → <math>f'(x)= 2\cdot(x-1)</math><br /> | ||
| + | |||
| + | 2. Schritt: Steigung der Tangenten in Punkt A: <math> f'(1,25)= 2\cdot(1,25-1)=0,5=m_1 </math><br /> | ||
| + | |||
| + | 3. Schritt: Steigung der Tangente g bestimmen → <math> 0,5 \cdot m_2 = -1 <=> m_2=-2 </math><br /> | ||
| + | |||
| + | 4. Schritt: Schnittstelle der Tangente g mit Graphen bestimmen: <math>f'(x)=-2=2\cdot(x-1)=2x-2 <=> x=0 </math><br /> | ||
| + | |||
| + | 5. Schritt: Schnittpunkt bestimmen: <math> f(0)=(0-1)^2+1=2 </math>, also <math>(0|2)</math><br /> | ||
| + | |||
| + | 6. Schritt: Tangentengleichung für g aufstellen: <math>g(x)=-2x+2</math>.<br /> | ||
| − | + | (y-Achsenabschnitt muss hier nicht extra bestimmt werden, da dies der Schnittpunkt mit dem Graphen ist.)</popup> | |
| − | + | ||
| − | + | ||
}} | }} | ||
| Zeile 79: | Zeile 106: | ||
Schaue dir das Applet an und entscheide auf Grundlage dessen, ob die unten stehenden Aussagen ''richtig'' oder ''falsch'' sind. | Schaue dir das Applet an und entscheide auf Grundlage dessen, ob die unten stehenden Aussagen ''richtig'' oder ''falsch'' sind. | ||
| − | ''Hinweis | + | ''Hinweis: Du kannst den Punkt P und auch die damit verbundene Tangente t selbst bewegen, um dir die Aussagen zu veranschaulichen. Oder du nutzt alternativ den eingebauten Regler.'' |
| − | <iframe scrolling="no" title="Lernpfad 1" src="https://www.geogebra.org/material/iframe/id/ | + | <iframe scrolling="no" title="Lernpfad 1" src="https://www.geogebra.org/material/iframe/id/vrcchyux/width/1522/height/585/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="950px" height="350px" style="border:0px;"> </iframe> |
<iframe src="https://learningapps.org/watch?v=pwhjkhu0j18" style="border:0px;width:70%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pwhjkhu0j18" style="border:0px;width:70%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| Zeile 94: | Zeile 121: | ||
Halte deine Überlegungen stichpunktartig fest und überprüfe diese anschließend anhand der unten stehenden Lösung. | Halte deine Überlegungen stichpunktartig fest und überprüfe diese anschließend anhand der unten stehenden Lösung. | ||
| − | <iframe scrolling="no" title="Lokale Linearität 2" src="https://www.geogebra.org/material/iframe/id/y4na67dt/width/1536/height/700/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="850px" height=" | + | <iframe scrolling="no" title="Lokale Linearität 2" src="https://www.geogebra.org/material/iframe/id/y4na67dt/width/1536/height/700/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="850px" height="470px" style="border:0px;"> </iframe> |
<popup name="Lösung"> Wenn du es im Applet ausprobiert hast, wirst du genau das sehen: Wenn man an einer Stelle der Funktion eine Tangente anlegt, stimmt diese in gewissem Maße mit dieser Funktion überein. Nämlich genau dann, wenn man ganz nah heranzoomt. Daher kann man auch die Tangentensteigung als Instrument zur Bestimmung der Steigung in einem Punkt (Ableitung) verwenden. </popup> | <popup name="Lösung"> Wenn du es im Applet ausprobiert hast, wirst du genau das sehen: Wenn man an einer Stelle der Funktion eine Tangente anlegt, stimmt diese in gewissem Maße mit dieser Funktion überein. Nämlich genau dann, wenn man ganz nah heranzoomt. Daher kann man auch die Tangentensteigung als Instrument zur Bestimmung der Steigung in einem Punkt (Ableitung) verwenden. </popup> | ||
}} | }} | ||
| − | {{Aufgaben|8: | + | {{Aufgaben|8: Besondere Punkte| |
| − | In der untenstehenden Grafik siehst du den Graph einer Funktion, sowie deren Punkt P. Bei P ist eine Tangente an die Funktion angelegt, | + | In der untenstehenden Grafik siehst du den Graph einer Funktion, sowie deren Punkt P. Bei P ist eine Tangente an die Funktion angelegt, erkennbar durch die rot gestrichelten Linien. Der Punkt lässt sich verschieben. Mithilfe des Buttons oben rechts im Applet lässt sich der Punkt zur ursprünglichen Position zurücksetzen. |
'''a)''' | '''a)''' | ||
| Zeile 111: | Zeile 138: | ||
| − | <iframe scrolling="no" title="Differenzierbarkeit von Funktionen" src="https://www.geogebra.org/material/iframe/id/mpgmucwe/width/700/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="700px" height=" | + | <iframe scrolling="no" title="Differenzierbarkeit von Funktionen" src="https://www.geogebra.org/material/iframe/id/mpgmucwe/width/700/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="700px" height="470px" style="border:0px;"> </iframe> |
<popup name="Tipp"> | <popup name="Tipp"> | ||
zu a) Mach dir klar, wie dir die eingezeichnete Tangente helfen kann. Wie hängt die Tangente mit der Ableitung zusammen? Dann kannst du die Lösung einfach ablesen. | zu a) Mach dir klar, wie dir die eingezeichnete Tangente helfen kann. Wie hängt die Tangente mit der Ableitung zusammen? Dann kannst du die Lösung einfach ablesen. | ||
| Zeile 118: | Zeile 145: | ||
<popup name="Lösung zu a)"> Steigung der Tangenten m=0,91, also gilt für die Ableitung der Funktion f in P: f'(0,54)=0,91. </popup> | <popup name="Lösung zu a)"> Steigung der Tangenten m=0,91, also gilt für die Ableitung der Funktion f in P: f'(0,54)=0,91. </popup> | ||
<popup name="Lösung zu b)"> Nein, es kann keine zwei verschiedenen Tangenten in einem Punkt geben. Für die Ableitung an dieser "Knickstelle" bedeutet dies, dass sie gar nicht existiert, eben da man keine eindeutige Tangente einzeichnen kann. Obwohl man die Ableitung an allen anderen Punkten der Funktion schon bilden kann, spricht man davon, dass die gesamte Funktion keine Ableitungsfunktion besitzt. Sie ist also "nicht differenzierbar". Es gibt außer dieser noch weitere Funktionen, für die dies gilt. </popup>}} | <popup name="Lösung zu b)"> Nein, es kann keine zwei verschiedenen Tangenten in einem Punkt geben. Für die Ableitung an dieser "Knickstelle" bedeutet dies, dass sie gar nicht existiert, eben da man keine eindeutige Tangente einzeichnen kann. Obwohl man die Ableitung an allen anderen Punkten der Funktion schon bilden kann, spricht man davon, dass die gesamte Funktion keine Ableitungsfunktion besitzt. Sie ist also "nicht differenzierbar". Es gibt außer dieser noch weitere Funktionen, für die dies gilt. </popup>}} | ||
| + | |||
| + | [[Kategorie:Digitale Werkzeuge in der Schule|!]] | ||
Aktuelle Version vom 28. Dezember 2018, 00:00 Uhr
|
Dieser Lernpfad beschäftigt sich mit der Steigung eines Funktionsgraphen in einem Punkt. In den Aufgaben 1 und 2 wird die grundlegende Vorstellung von Sekanten und Tangenten behandelt. In den Aufgaben 3, 4 und 5 geht es darum Tangentengleichungen und Normalengleichungen aufzustellen. Aufgabe 6 behandelt den Zusammenhang der Steigung und der Ableitung in einem Punkt. Bei den Aufgaben 7 und 8 handelt es sich um Forderaufgaben im Bereich lokale Linearität und Ableitung in besonderen Punkten. |
Inhaltsverzeichnis |
Unterscheidung Tangente und Sekante
|
|
|
In diesem Applet siehst du den Graphen einer Funktion f und eine Gerade a. Weiterhin findest du in diesem zwei Regler, an denen du x0 und h einstellen kannst.
Hinweis: Beachte hier, dass die Dezimalzahlen mit Punkt und nicht wie gewohnt mit Komma geschrieben werden. Verwende für das Ausfüllen der Lücken bitte die folgende Schreibweise für Koordinaten: "(x/y)".
|
Tangentengleichungen aufstellen
|
Die Tangente an die Funktion |
|
Bestimme die Gleichung der Tangente an die Funktion
|
|
|
|
Schaue dir das Applet an und entscheide auf Grundlage dessen, ob die unten stehenden Aussagen richtig oder falsch sind. Hinweis: Du kannst den Punkt P und auch die damit verbundene Tangente t selbst bewegen, um dir die Aussagen zu veranschaulichen. Oder du nutzt alternativ den eingebauten Regler.
|
Forderaufgaben
|
In der Abbildung siehst du eine Funktion, sowie eine Tangente dieser Funktion im Punkt A. Mit dem Schieberegler kannst du an der markierten Stelle ran- und rauszoomen. Der rot markierte Ausschnitt ist auf der rechten Seite der Abbildung vergrößert dargestellt. Probiere zunächst aus, was passiert, wenn du ganz nah reinzoomst und den Ausschnitt so weit es geht vergrößerst. Bewerte folgende Aussage: "Wenn man sehr stark zoomt, stimmt die Funktion an der Stelle A mit der Tangente überein". Was hast du gesehen? Stimmst du zu? Wenn ja, warum? Halte deine Überlegungen stichpunktartig fest und überprüfe diese anschließend anhand der unten stehenden Lösung. |
|
In der untenstehenden Grafik siehst du den Graph einer Funktion, sowie deren Punkt P. Bei P ist eine Tangente an die Funktion angelegt, erkennbar durch die rot gestrichelten Linien. Der Punkt lässt sich verschieben. Mithilfe des Buttons oben rechts im Applet lässt sich der Punkt zur ursprünglichen Position zurücksetzen. a) Bestimme mithilfe der Abbildung durch genaues Hinsehen die Ableitung der Funktion im Punkt P.
Versuche nachzuvollziehen was Lisa meint, indem du wie sie den Punkt P verschiebst. Kann das überhaupt sein? Wie würdest du Lisas Frage beantworten?
|
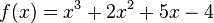 im Punkt
im Punkt 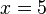 soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
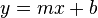 , wobei
, wobei 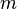 die Steigung der Tangente ist und
die Steigung der Tangente ist und 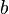 der y-Achsenabschnitt.
der y-Achsenabschnitt.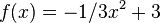 im Punkt
im Punkt 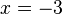 .
.
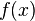 ist
ist 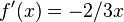 .
.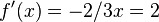 .
.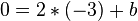 , also
, also 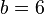 .
.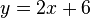 .
.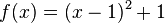 so, dass die Tangente g senkrecht zur Tangente a an der Stelle 1,25 (Punkt A) ist. Notiere deine einzelnen Rechenschritte in deinem Heft.
so, dass die Tangente g senkrecht zur Tangente a an der Stelle 1,25 (Punkt A) ist. Notiere deine einzelnen Rechenschritte in deinem Heft.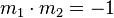 gilt, so stehen die Geraden senkrecht aufeinander. (Mit
gilt, so stehen die Geraden senkrecht aufeinander. (Mit 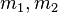 sind die beiden Steigungen der Geraden gemeint.)
sind die beiden Steigungen der Geraden gemeint.)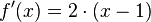
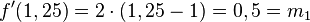
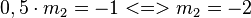
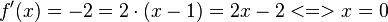
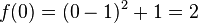 , also
, also 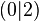
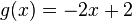 .
.
