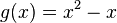Achtung:

Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.

Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.

Gerne kannst Du natürlich weiterarbeiten

im neuen Projektwiki (projekte.zum.de).

Verschieben und Strecken: Unterschied zwischen den Versionen

Aus Projektwiki - ein Wiki mit Schülern für Schüler.
Wechseln zu: Navigation, Suche
 
(5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
{{Merke|<iframe width="560" height="315" src="https://www.youtube.com/embed/9wdQGr_-P8A" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>}}
 
{{Merke|<iframe width="560" height="315" src="https://www.youtube.com/embed/9wdQGr_-P8A" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>}}
  
−
{{Aufgaben|1|
+
{{Aufgaben|1 Strecken von Graphen| Nachfolgend seht ihr die Funktion <math>f(x)=x^3-2x^2+1</math>. Probiere mit den Schiebereglern aus, wie sich die Funktion verändert und beantworte anschließend die Fragen unterhalb des Graphen.
−
Im folgenden siehst du die Funktion <math>a(x-b)^2+c</math>. Probiere mit den Schiebereglern aus, wie sich die Funktion verändert und beantworte anschließend die Fragen unterhalb des Graphen.
+
<iframe scrolling="no" title="Verschiebung" src="https://www.geogebra.org/material/iframe/id/sgr6ncfe/width/700/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="700px" height="500px" style="border:0px;"> </iframe>
  
−
<iframe scrolling="no" title="Verschieben und Strecken" src="https://www.geogebra.org/material/iframe/id/m73rjhs7/width/1241/height/541/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1000px" height="541px" style="border:0px;"> </iframe>
+
<iframe src="https://learningapps.org/watch?v=pc5qtwm6n19" style="border:0px;width:70%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}}
  
−
<iframe src="https://learningapps.org/watch?v=pnpj7d5j319" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>
+
{{Aufgaben|2 Verschieben von Graphen| Wieder seht ihr die Funktion <math>f(x)=x^3-2x^2+1</math>. Geh genauso wie in Aufgabe 1 vor und beantworte den untenstehenden Lückentext.
−
}}
+
<iframe scrolling="no" title="Verschieben" src="https://www.geogebra.org/material/iframe/id/fjwfgfku/width/700/height/500/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="700px" height="500px" style="border:0px;"> </iframe>
 +
 
 +
<iframe src="https://learningapps.org/watch?v=ps7xnkspn19" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}}
  
−
{{Aufgaben|2| Der Graph von f soll im Folgenden verschoben und/oder gestreckt werden. Gebt dazu den zugehörigen Term an.
+
{{Aufgaben|3| Der Graph von f soll im Folgenden verschoben und/oder gestreckt werden. Gebt dazu den zugehörigen Term an.
  
 
'''Beispiel:''' <math>f(x)=x^2</math> soll um eine Einheit nach rechts und zwei Einheiten nach oben verschoben werden. Der neue Term lautet: <math>g(x)=f(x-1)+2=(x-1)^2+2</math>
 
'''Beispiel:''' <math>f(x)=x^2</math> soll um eine Einheit nach rechts und zwei Einheiten nach oben verschoben werden. Der neue Term lautet: <math>g(x)=f(x-1)+2=(x-1)^2+2</math>
Zeile 27: Zeile 29:
 
}}
 
}}
  
−
{{Aufgaben|3| Durch welche Verschiebungen/Streckungen ist der Graph der Funktion g aus dem Graphen der Funktion f entstanden?
+
{{Aufgaben|4| Durch welche Verschiebungen/Streckungen ist der Graph der Funktion g aus dem Graphen der Funktion f entstanden?
  
 
'''a)''' <math>f(x)=3x^3+5x</math> und <math>g(x)=-x^3-5/3x</math>
 
'''a)''' <math>f(x)=3x^3+5x</math> und <math>g(x)=-x^3-5/3x</math>

Aktuelle Version vom 13. November 2019, 17:45 Uhr

Nuvola apps kig.png   Merke

Stift.gif   Aufgabe 1 Strecken von Graphen 
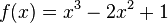Nachfolgend seht ihr die Funktion f(x)=x^3-2x^2+1. Probiere mit den Schiebereglern aus, wie sich die Funktion verändert und beantworte anschließend die Fragen unterhalb des Graphen.

Stift.gif   Aufgabe 2 Verschieben von Graphen 
Wieder seht ihr die Funktion f(x)=x^3-2x^2+1. Geh genauso wie in Aufgabe 1 vor und beantworte den untenstehenden Lückentext.

Stift.gif   Aufgabe 3 
Der Graph von f soll im Folgenden verschoben und/oder gestreckt werden. Gebt dazu den zugehörigen Term an.

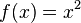Beispiel: f(x)=x^2 soll um eine Einheit nach rechts und zwei Einheiten nach oben verschoben werden. Der neue Term lautet: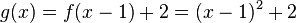 g(x)=f(x-1)+2=(x-1)^2+2

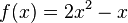a) f(x)=2x^2-x soll um drei Einheiten nach links und eine Einheit nach unten verschoben werden.

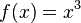b) f(x)=x^3 soll um eine Einheit nach oben verschoben und mit dem Faktor zwei gestreckt werden.

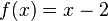c) f(x)=x-2 soll um 2 Einheiten nach rechts verschoben und an der x-Achse gespiegelt werden.

Stift.gif   Aufgabe 4 
Durch welche Verschiebungen/Streckungen ist der Graph der Funktion g aus dem Graphen der Funktion f entstanden?

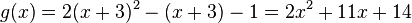
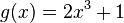
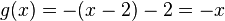
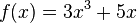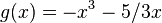
a) f(x)=3x^3+5x und g(x)=-x^3-5/3x

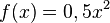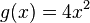
b) f(x)=0,5x^2 und g(x)=4x^2

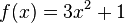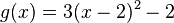
c) f(x)=3x^2+1 und g(x)=3(x-2)^2-2

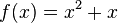d) f(x)=x^2+x und g(x)=x^2-x


Von „https://projektwiki.zum.de/index.php?title=Praxissemester_Pieper/Klausurvorbereitung_EF/Verschieben_und_Strecken&oldid=77310“