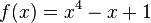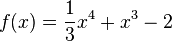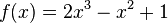Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Gemischte Aufgaben: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
(Die Seite wurde neu angelegt: „{{Aufgaben|1 Graphen skizzieren| Skizziere folgende Graphen. Achte dabei auf das Verhalten nahe Null und gegen Unendlich sowie auf die Symmetrie. '''a)''' <ma…“) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
'''a)''' | '''a)''' | ||
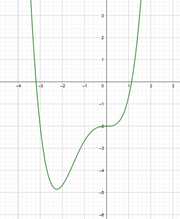
| − | <math>x^4-x+1</math> | + | <math>f(x)=x^4-x+1</math> |
'''b)''' | '''b)''' | ||
| + | <math>f(x)=\frac{1}{3}x^4+x^3-2</math> | ||
'''c)''' | '''c)''' | ||
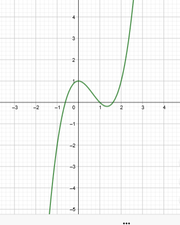
| + | <math>f(x)=2x^3-x^2+1</math> | ||
| − | <popup Name="Lösung">a) [[Datei:Geogebra7.png|miniatur|links]]</popup> | + | |
| + | <popup Name="Lösung"> | ||
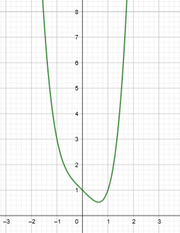
| + | a) [[Datei:Geogebra7.png|miniatur|links]] | ||
| + | |||
| + | b) [[Datei:Geobebra6.png|miniatur]] | ||
| + | |||
| + | c) [[Datei:Geogebra9.png|miniatur|rechts]] | ||
| + | </popup> | ||
| + | }} | ||
| + | |||
| + | {{Aufgaben|2 Funktionsgleichung aufstellen| Bestimme mit den gegebenen Eigenschaften eine passende Funktionsgleichung einer ganzrationalen Funktion. | ||
| + | |||
| + | '''a)''' | ||
| + | Die Funktion ist punksymmetrisch zum Ursprung und der Grad von f ist kleiner als 4. | ||
| + | |||
| + | '''b)''' | ||
| + | Die Funktion ist achsensymmetrisch zur y-Achse, hat mindestens Grad 3 und besitzt keine Nullstellen. | ||
| + | |||
| + | '''c)''' | ||
| + | |||
| + | <popup Name="Lösung"> | ||
| + | '''a)''' | ||
| + | z.B. f(x)=x^3 | ||
| + | |||
| + | '''b)''' | ||
| + | z.B. f(x)=x^4+1 | ||
| + | |||
| + | '''c)''' | ||
| + | </popup> | ||
}} | }} | ||
Aktuelle Version vom 13. November 2019, 16:45 Uhr
Skizziere folgende Graphen. Achte dabei auf das Verhalten nahe Null und gegen Unendlich sowie auf die Symmetrie. a)
b)
c)
|
Bestimme mit den gegebenen Eigenschaften eine passende Funktionsgleichung einer ganzrationalen Funktion. a) Die Funktion ist punksymmetrisch zum Ursprung und der Grad von f ist kleiner als 4. b) Die Funktion ist achsensymmetrisch zur y-Achse, hat mindestens Grad 3 und besitzt keine Nullstellen. c) |