Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Nullstellen: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{Aufgaben|1|<iframe src="https://learningapps.org/watch?v=p3f5jydgt19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>}} | + | {{Aufgaben|1|<iframe src="https://learningapps.org/watch?v=p3f5jydgt19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> |
| + | |||
| + | <popup Name="Lösung"> | ||
| + | <math>x^2-x+2=0</math> --> pq-Formel | ||
| + | |||
| + | <math>x^4+3x^2-9=0</math> --> Substitution, dann pq-Formel | ||
| + | |||
| + | <math>6x^3-3x^2=0</math> --> Ausklammern von <math>x^2</math>, dann einfaches Umformen | ||
| + | |||
| + | <math>(x-2)(x+3)=0</math> --> Ablesen | ||
| + | |||
| + | <math>x^6-4x^3+1=0</math> --> Substitution, dann pq-Formel | ||
| + | |||
| + | <math>4x^4-8x^3+2x^2=0</math> --> Ausklammern, dann pq-Formel</popup>}} | ||
{{Aufgaben|2| | {{Aufgaben|2| | ||
<iframe src="https://learningapps.org/watch?v=pc6u934vj19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pc6u934vj19" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| − | <popup Name="Tipp">Ihr kennt | + | <popup Name="Tipp">Ihr kennt verschiedene Verfahren, die bei der Nullstellenberechnung helfen: Ablesen, Ausklammern, Substitution, einfaches Umformen und pq-Formel. </popup> |
<popup Name="Tipp">Einmal können euch die binomischen Formeln weiterhelfen. </popup> | <popup Name="Tipp">Einmal können euch die binomischen Formeln weiterhelfen. </popup> | ||
<popup Name="Lösung"><math>f(x)=(x-3)(x-1)^2</math> hat die Nullstellen: (3,0),(1,0) | <popup Name="Lösung"><math>f(x)=(x-3)(x-1)^2</math> hat die Nullstellen: (3,0),(1,0) | ||
| − | <math> | + | <math>f(x)=x^4+4x^2</math> hat die Nullstellen (0,0),(-2,0),(2,0) |
| + | |||
| + | <math>f(x)=x^4-3x^2-4</math> hat die Nullstellen (2,0),(-2,0) | ||
| + | |||
| + | <math>f(x)=x^2-x-12</math> hat die Nullstellen (-3,0),(4,0) | ||
| + | |||
| + | <math>f(x)=x^3-x^2-6x</math> hat die Nullstellen (0,0),(-2,0),(3,0) | ||
| + | |||
| + | <math>f(x)=(x-1)(2x^2-8)</math> hat die Nullstellen (1,0),(-2,0),(2,0) | ||
| + | |||
| + | </popup> | ||
<popup Name="weitere Übung">Das Thema Nullstellen findet sich im Buch auf S. 26ff.</popup> | <popup Name="weitere Übung">Das Thema Nullstellen findet sich im Buch auf S. 26ff.</popup> | ||
| Zeile 34: | Zeile 57: | ||
}} | }} | ||
| − | {{Aufgaben|4| Gebe eine ganzrationale Funktion | + | {{Aufgaben|4| Gebe eine ganzrationale Funktion vierten Grades an, die die angegebenen Nullstellen besitzt. |
'''a)''' 1 und -1 | '''a)''' 1 und -1 | ||
'''b)''' -2, 0 und 1 | '''b)''' -2, 0 und 1 | ||
| + | |||
| + | '''c)'''-3, 1, 2 und 4 | ||
<popup Name="Tipp">Verwende die Idee, dass man bei der Darstellung in Linearfaktoren die Nullstellen direkt ablesen kann.</popup> | <popup Name="Tipp">Verwende die Idee, dass man bei der Darstellung in Linearfaktoren die Nullstellen direkt ablesen kann.</popup> | ||
<popup Name="Lösung"> | <popup Name="Lösung"> | ||
| − | '''a)''' <math>f(x)=(x-1)(x+1) | + | '''a)''' z.B. <math>f(x)=(x-1)^2(x+1)^2</math> |
| − | '''b)''' <math>f(x)=(x+2) | + | '''b)''' z.B. <math>f(x)=(x+2)^2x(x-1)=x^3+x^2-x</math> |
| + | '''c)''' z.B. <math>f(x)=(x+3)(x-1)(x-2)(x-4)</math></popup> | ||
}} | }} | ||
Aktuelle Version vom 27. November 2019, 09:47 Uhr
|
|
|
|
Bestimme die Nullstellen der Funktion f. a) b) c) d)
|
Gebe eine ganzrationale Funktion vierten Grades an, die die angegebenen Nullstellen besitzt. a) 1 und -1 b) -2, 0 und 1 c)-3, 1, 2 und 4 |
|
|
30px Merke
|
30px Merke
|
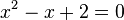 --> pq-Formel
--> pq-Formel
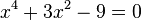 --> Substitution, dann pq-Formel
--> Substitution, dann pq-Formel
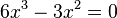 --> Ausklammern von
--> Ausklammern von 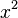 , dann einfaches Umformen
, dann einfaches Umformen
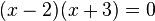 --> Ablesen
--> Ablesen
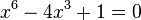 --> Substitution, dann pq-Formel
--> Substitution, dann pq-Formel
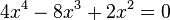 --> Ausklammern, dann pq-Formel
--> Ausklammern, dann pq-Formel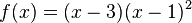 hat die Nullstellen: (3,0),(1,0)
hat die Nullstellen: (3,0),(1,0)
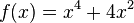 hat die Nullstellen (0,0),(-2,0),(2,0)
hat die Nullstellen (0,0),(-2,0),(2,0)
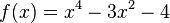 hat die Nullstellen (2,0),(-2,0)
hat die Nullstellen (2,0),(-2,0)
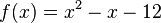 hat die Nullstellen (-3,0),(4,0)
hat die Nullstellen (-3,0),(4,0)
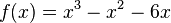 hat die Nullstellen (0,0),(-2,0),(3,0)
hat die Nullstellen (0,0),(-2,0),(3,0)
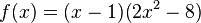 hat die Nullstellen (1,0),(-2,0),(2,0)
hat die Nullstellen (1,0),(-2,0),(2,0)
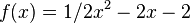
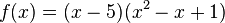
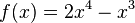
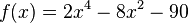
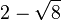 und
und 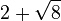
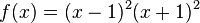
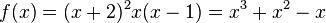
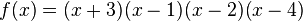
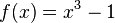
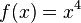 hat nur eine Nullstelle (x=0).
hat nur eine Nullstelle (x=0).