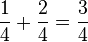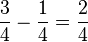Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Addition und Subtraktion gleichnamiger Brüche: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 28: | Zeile 28: | ||
[http://Subtraktion Subtraktion gleichnamiger Brüche <iframe src="https://learningapps.org/watch?v=phm8i3xak18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>] | [http://Subtraktion Subtraktion gleichnamiger Brüche <iframe src="https://learningapps.org/watch?v=phm8i3xak18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>] | ||
| + | |||
| + | Addition und Subtraktion von Brüchen: | ||
| + | |||
| + | <div class="zuordnungs-quiz"> | ||
| + | |||
| + | {| | ||
| + | | <math>x +\frac{28}{31}=\frac{40}{31}</math> | | ||
| + | | <math>\frac{12}{31} </math> | ||
| + | |- | ||
| + | | <math>x +\frac{6}{15}=\frac{18}{15}</math> | | ||
| + | | <math>\frac{12}{15} </math> | ||
| + | |- | ||
| + | | <math>x -\frac{2}{22}=\frac{15}{22}</math> | | ||
| + | | <math>\frac{17}{22} </math> | ||
| + | |} | ||
| + | |||
| + | </div> | ||
Version vom 3. Januar 2018, 16:05 Uhr
Addition und Subtraktion gleichnamiger Brüche
Unter dem Begriff gleichnamige Brüche versteht man Brüche, die den gleichen Nenner haben.
1. Addition gleichnamiger Brüche
Du addierst Brüche, indem du nur die Zähler addierst. Die Nenner bleiben unverändert.
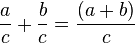
Beispiel:
2. Subtraktion gleichnamiger Brüche
Du subtrahierst Brüche, indem du nur die Zähler subtrahierst. Die Nenner bleiben unverändert.
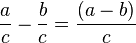
Beispiel:
Übungen zur Addition un Subtraktion gleichnamiger Brüche:
Subtraktion gleichnamiger Brüche
Addition und Subtraktion von Brüchen:
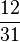
| |
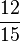
| |
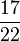
|