Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Rechnen mit rationalen Zahlen: Unterschied zwischen den Versionen
| Zeile 79: | Zeile 79: | ||
:-> bei gleichen Vorzeichen:'''<span style="color: #EE1289"> + </span>''' | :-> bei gleichen Vorzeichen:'''<span style="color: #EE1289"> + </span>''' | ||
| − | :-> bei ungleichen Vorzeichen: '''<span style="color: #EE1289"> | + | :-> bei ungleichen Vorzeichen: '''<span style="color: #EE1289"> − </span>''' |
| Zeile 91: | Zeile 91: | ||
:-> bei gleichen Vorzeichen:'''<span style="color: #EE1289"> + </span>''' | :-> bei gleichen Vorzeichen:'''<span style="color: #EE1289"> + </span>''' | ||
| − | :-> bei ungleichen Vorzeichen: '''<span style="color: #EE1289"> | + | :-> bei ungleichen Vorzeichen: '''<span style="color: #EE1289"> − </span>''' |
| Zeile 112: | Zeile 112: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Welche Zahl muss man zu ( | + | Welche Zahl muss man zu (−3,4) addieren um 5 zu erhalten? '''8,4''' |
| − | Welche Zahl muss man von 2,7 subtrahieren um ( | + | Welche Zahl muss man von 2,7 subtrahieren um (−1) zu erhalten?'''−3,7''' |
Welche Zahl muss man zu <math>\frac{4} {8}</math> addieren um 1 zu erhalten? '''<math>\frac{2}{4}</math>''' | Welche Zahl muss man zu <math>\frac{4} {8}</math> addieren um 1 zu erhalten? '''<math>\frac{2}{4}</math>''' | ||
| − | Welche Zahl muss man zu <math> | + | Welche Zahl muss man zu <math>−2\frac{2} {4}</math> addieren um (−1) zu erhalten? '''<math>\frac{7} {2}</math>''' |
| − | Welche Zahl muss man durch <math> | + | Welche Zahl muss man durch <math>−\frac{4} {7}</math> dividieren um <math>\frac{1}{2}</math> zu erhalten?'''<math>\frac{8}{7}</math>''' |
| − | Welche Zahl muss man mit 0,5 multiplizieren um <math> | + | Welche Zahl muss man mit 0,5 multiplizieren um <math>−\frac{1}{2}</math> zu erhalten? '''−1''' |
Version vom 31. März 2018, 13:09 Uhr
Was sind rationale Zahlen?
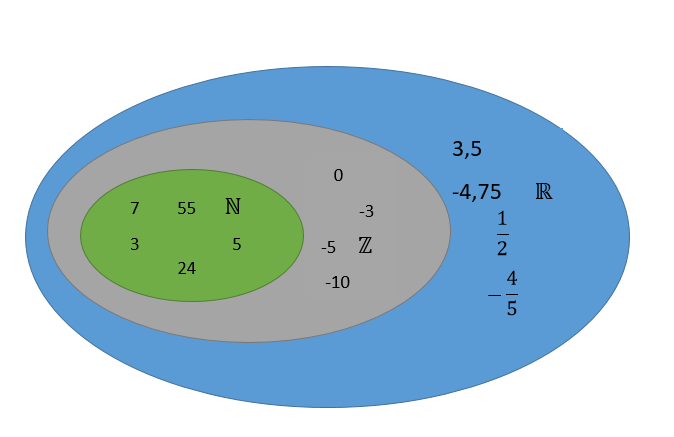
Unter rationalen Zahlen versteht man alle dir bereits bekannten "ganzen Zahlen" (Z)
Zu den rationalen Zahlen (Q) gehören jetzt aber außerdem noch Brüche und Dezimalzahlen.
Bsp. zu Brüchen:  oder
oder 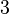

Bsp. zu Dezimalzahlen: 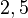 oder (
oder (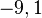 )
)
1. Die Menge der rationalen Zahlen
Beachte: Die Division mit rationalen Zahlen ist nun auch möglich, wenn der Dividend kein ganzzahliges Vielfaches des Divisors ist. Durch die Zahl 0 darf jedoch immer noch nicht dividiert werden!
Verschiedene Schreibweisen:  =
= 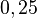 =
= 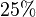
Alle Darstellungsformen sind mathematisch korrekt und bedeuten das Gleiche. Je nach Aufgabenstellung könnt ihr die Zahlen nach Belieben umformen.
Verstanden? Dann ordne doch die unten stehen Zahlen passend zu den bereits vorgegeben Zahlen der jeweils anderen Schreibweisen zu.
| 0,2 | 20% | 
|
| 80% | 0,8 | 
|
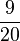 |
45% | 0,45 |
2. Rechnen mit rationalen Zahlen
Für das Rechnen mit rationalen Zahlen gelten die gleichen Regeln wie für das Rechnen mit ganzen Zahlen.
|
Zur Erinnerung
1. Addition Gleiche Vorzeichen: addieren und Vorzeichen in die Summe übernehmen Verschiedene Vorzeichen: Vorzeichen des größeren Betrags in die Summe übernehmen
kleineren Betrag vom größeren subtrahieren falls andersrum, dann hat das Ergebnis ein -
multipliziere die Faktoren
dividiere die Faktoren
|
Hier hast du noch Aufgaben um das Gelernte anzuwenden. Viel Spaß:)
| zum Oberflächeninhalt | zu Rechenvorteilen |
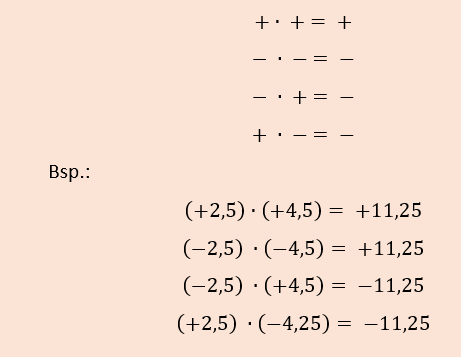
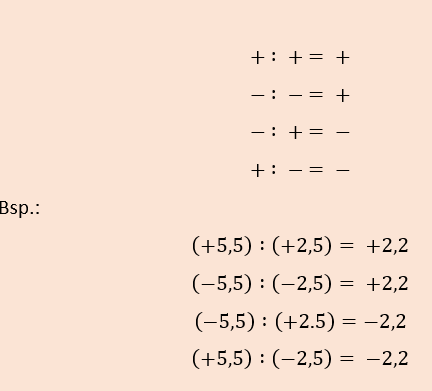
 addieren um 1 zu erhalten?
addieren um 1 zu erhalten? 



