Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Grenzwerte im Unendlichen: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält.<br /> | Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält.<br /> | ||
| − | ''Anschaulich gesprochen:'' Man betrachtet | + | ''Anschaulich gesprochen:'' Man betrachtet den Funktionsgraphen am rechen und linken Bildrand. |
Bei [http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Grenzwerte_im_Unendlichen/Wiederholung:Ganzrationale_Funktionen ganzrationalen Funktionen] hast du bereits vier Fälle über den charakteristischen Verlauf einer Funktion kennen gelernt.<br /> | Bei [http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Grenzwerte_im_Unendlichen/Wiederholung:Ganzrationale_Funktionen ganzrationalen Funktionen] hast du bereits vier Fälle über den charakteristischen Verlauf einer Funktion kennen gelernt.<br /> | ||
| + | |||
Auch mit dem Verhalten von gebrochen rationalen Funktionen für immer größer werdende x- Werte hast du dich schon auseinandergesetzt.<br /> | Auch mit dem Verhalten von gebrochen rationalen Funktionen für immer größer werdende x- Werte hast du dich schon auseinandergesetzt.<br /> | ||
| − | Wie verhält sich die Funktion f: x -> | + | ''Hierfür ein Beispiel:'' |
| + | Wie verhält sich die Funktion f: x -> <math>\frac{4x-3}{x}</math> für immer größer werdende x- Werte?<br /> | ||
| + | Fülle die '''Wertetabelle''' vollständig aus, indem du die Funktionswerte in das jeweilige Feld eingibst und "Enter" drückst.<br /> | ||
| + | Wenn sich das Feld grün färbt, war deine Eingabe richtig; bei orange hast du einen Fehler gemacht.<br /> | ||
| + | |||
| + | Übertrage die berechneten Punkte in das '''GeoGebra-Applet''' und skizziere den Verlauf des Funktionsgraphen von f.<br /> | ||
| + | |||
| + | Wie verhält sich die Funktion für immer größer, bzw. immer kleiner werdende x- Werte? | ||
| + | |||
| + | {| | ||
| + | |valign="top" width="34%"|<iframe src="http://LearningApps.org/watch?v=pvu3bym5c" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| + | |||
| + | |<ggb_applet width="689" height="483" version="4.2" ggbBase64="UEsDBBQACAAIAAa/vUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAAa/vUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVfrb9s2EP+c/hUHfU5sPkRKKuwWbYECBdKhWLqh2zdaYmQusihI9GvoH78jKTlO2gxrAwyJfXzc63e8O9KL14dNAzvdD8a2y4TOSAK6LW1l2nqZbN3tVZ68fvViUWtb61Wv4Nb2G+WWSTpjyb0czmZp5oVNtUwyWlW3K5VeKanVVcqK8qpgKruqKi2pqhivcp0AHAbzsrW/qI0eOlXqm3KtN+ralsoFnWvnupfz+X6/n03WZ7av53W9mh2GKgH0vB2WyTh4ieoeCO15YGeE0PmXj9dR/ZVpB6faEu17VFvz6sXFYm/ayu5hbyq39t7nCay1qdcIUwiEOfdMHWLtdOnMTg8oejYNmN2mSwKbav3+RRxBc4KTQGV2ptL9MiEzluVCUMEZ4TxlEm3Y3ujWjbx0tDmftC12Ru+jWj8KFlNSZHgEZjCrRi+TW9UMiMq0tz1GFB3qtzgd3LHRK9VP83t/6CX+IYP5W3tdeHQxDMskzy+p5JcZIZdCkOjKud0EnLVNUEpAFPD1KzDCCFx6QiNhSKSMWySuER4JiySNRESeNIqnkTWNPGnkSfm/wBzn9zjHhQdAJ5j8HCZFfP4j8RPwP8KZn+GkHsRXoN77QDh4v2nw35N0nMo4zQKhJBI6bub+K8RLPhMR/ylE9MxqTIenjX6TLpNFmRf/3SJ7Fs4TSvY9lEw8gfKZwZ2MUnFmFG2F//D5xiT/IZxPhvYHLMr0OaX/EwYz8n8YXMynRrcYaw+Gtecd09XpzeC7Di9C4wEKAgtTZtgnBNACSeYLlAEVkAqc0hykpxlwX5MpcMjB81EOob2IHL/SUK8SBOryi1ksXOApCA40NKUUsBVBaGzY5BhHDiFAoJC3Tr1ZLiGVOOE5pOigb2mZbxsc5XCOxhlwCtzL0gyYBMkg822Rpr5bytz7jkoZSALSi2JfxJ4Y+yFK5MA9Gszwzg7mFNy1brrTqYQ4mrbbujF243q5qaY4OvuIvbLl3dtHwdZqcNMYmfAyur/y4uX04Ea8WDRqpRt8N9z4PADYqcaXcNB/a1sHUw7kca3uVbc25XCjnUOpAf5SO3WtnD68R+5hcjCYDhf1Qm/LxlRGtb9jkngVXiFM93ZoTNO9nRIRrZTW9tXNccDMgcOfurfoU4oXcE4ElVlBhWRYvMdxhxB8xmRcCsmLTLBMYOKWqgktaCYYowXmW5pnMsP6Oz6xxWU0rXcnaOqghymWdW+q8/GH4a1tqtN5dNa07p3q3LYPbzBsgr3H9KatGx1CG9oqvmbKu5U93MSY8qjr87HDGYn2V/U729gesCCZQCT1SFeRBh7v2ImLBB4SOMh0SKY67dOCBY5AV5EGLjz16NoIlE4oKZnMmCG0EVR+nmMhZZbJIYFta9x1nGF+mvJuhEqjwC/bzQrTbZR7qJN+V+fxZ3R6r/GdNrgv41vYj/84G39ea6f8C04wLoo8ywR+syLPY54+ytDFne5b3cQ8bDEVtnY7xMI4JffFYjvoT8qt37TVr7rGkv6kfFd16FpkvXev0qXZoGBcH4OvfGL8hlDjaqXrXk8hasKzOR5N2CXnVfHNclD1vrebD+3uM2bdI1cX8wnPYih70/nchhW2+Tt9n78YJYWXRHUuh+AHRFH6hoUH4fwhNFr3CaitW1tMrY/H3qgNXKMHqAKbAMIr4KMy2HQxub3tcyWhJ4w/Cl79A1BLBwg0pycq+QQAAMQMAABQSwECFAAUAAgACAAGv71C1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAAa/vUI0pycq+QQAAMQMAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAkAUAAAAA" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | ||
| + | |} | ||
Version vom 29. Mai 2013, 23:13 Uhr
Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält.
Anschaulich gesprochen: Man betrachtet den Funktionsgraphen am rechen und linken Bildrand.
Bei ganzrationalen Funktionen hast du bereits vier Fälle über den charakteristischen Verlauf einer Funktion kennen gelernt.
Auch mit dem Verhalten von gebrochen rationalen Funktionen für immer größer werdende x- Werte hast du dich schon auseinandergesetzt.
Hierfür ein Beispiel:
Wie verhält sich die Funktion f: x ->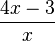 
für immer größer werdende x- Werte?
Fülle die Wertetabelle vollständig aus, indem du die Funktionswerte in das jeweilige Feld eingibst und "Enter" drückst.
Wenn sich das Feld grün färbt, war deine Eingabe richtig; bei orange hast du einen Fehler gemacht.
Übertrage die berechneten Punkte in das GeoGebra-Applet und skizziere den Verlauf des Funktionsgraphen von f.
Wie verhält sich die Funktion für immer größer, bzw. immer kleiner werdende x- Werte?
