Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Grenzwerte im Unendlichen: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
<center><table border="0" width="950px" cellpadding=5 cellspacing=15> | <center><table border="0" width="950px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | <big>Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält.<br /> | + | <big>Bearbeite parallel zum Lernpfad das [http://wikis.zum.de/projektwiki/Datei:AB_Grenzwerte.pdf Arbeitsblatt] zum Thema "Grenzwerte im Unendlichen".<br /> |
| + | <br /> | ||
| + | Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält.<br /> | ||
''Anschaulich gesprochen:'' Man betrachtet den Funktionsgraphen am rechten und linken Bildrand. | ''Anschaulich gesprochen:'' Man betrachtet den Funktionsgraphen am rechten und linken Bildrand. | ||
| Zeile 12: | Zeile 14: | ||
Auch mit dem Verhalten von gebrochen rationalen Funktionen für immer größer werdende x- Werte hast du dich schon auseinandergesetzt.<br /> | Auch mit dem Verhalten von gebrochen rationalen Funktionen für immer größer werdende x- Werte hast du dich schon auseinandergesetzt.<br /> | ||
| − | Dieses Wissen wird jetzt noch weiter vertieft. | + | Dieses Wissen wird jetzt noch weiter vertieft.<br /> |
| + | |||
| Zeile 32: | Zeile 35: | ||
*Über die beiden Kontrollkästchen lässt sich der '''<span style="color: #3A5FCD ">Graph der Funktion f</span>''' und die '''<span style="color: #EE7600 ">Gerade</span>''', an die sich '''<span style="color: #3A5FCD ">f</span>''' annähert, anzeigen. | *Über die beiden Kontrollkästchen lässt sich der '''<span style="color: #3A5FCD ">Graph der Funktion f</span>''' und die '''<span style="color: #EE7600 ">Gerade</span>''', an die sich '''<span style="color: #3A5FCD ">f</span>''' annähert, anzeigen. | ||
*Mit dem letzten Symbol "Verschiebe Zeichenblatt" in der Werkzeugleiste kannst du dir die beiden Graphen auch über den eigentlichen Bildrand hinweg anschauen. | *Mit dem letzten Symbol "Verschiebe Zeichenblatt" in der Werkzeugleiste kannst du dir die beiden Graphen auch über den eigentlichen Bildrand hinweg anschauen. | ||
| − | *Unter dem gleichen Symbol lässt sich auch das Werkzeug "Vergrößere" auswählen.<br />Sieh dir genau an, ob sich die beiden Graphen berühren!</big> | + | *Unter dem gleichen Symbol lässt sich auch das Werkzeug "Vergrößere" auswählen.<br />Sieh dir genau an, ob sich die beiden Graphen berühren! |
| + | *Übertrage den Graphen der Funktion f, sowie die Gerade in das Koordinatensystem auf deinem Arbeitsblatt. | ||
| + | </big> | ||
|} | |} | ||
| Zeile 43: | Zeile 48: | ||
<big> | <big> | ||
| − | Diese Vermutung lässt sich mathematisch untersuchen | + | Diese Vermutung lässt sich mathematisch untersuchen, wobei es hier hilfreich ist, f als Differenz zu schreiben.<br /> |
| + | Halte die wichtigsten Ergebnisse dabei auf deinem Arbeitsblatt fest.<br /> | ||
<br /> | <br /> | ||
| + | |||
'''<span style="color: #3A5FCD ">f (x)</span>''' = <math>\frac{4x-3}{x}</math> = <math>\frac{4x}{x}</math> - <math>\frac{3}{x}</math> = '''<span style="color: #EE7600 ">4</span>''' - <math>\frac{3}{x}</math><br /> | '''<span style="color: #3A5FCD ">f (x)</span>''' = <math>\frac{4x-3}{x}</math> = <math>\frac{4x}{x}</math> - <math>\frac{3}{x}</math> = '''<span style="color: #EE7600 ">4</span>''' - <math>\frac{3}{x}</math><br /> | ||
<br /> | <br /> | ||
| Zeile 112: | Zeile 119: | ||
</popup> | </popup> | ||
<br /> | <br /> | ||
| + | <big>Fülle den Lückentext aus und übertrage die kontrollierten Antworten auf dein Arbeitsblatt.</big><br /> | ||
| + | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
<u><big>Allgemein gilt:</big></u><br /> | <u><big>Allgemein gilt:</big></u><br /> | ||
| Zeile 153: | Zeile 162: | ||
}} | }} | ||
|} | |} | ||
| − | |||
Version vom 17. Juli 2013, 17:03 Uhr
|
Bearbeite parallel zum Lernpfad das Arbeitsblatt zum Thema "Grenzwerte im Unendlichen". Bei ganzrationalen Funktionen hast du bereits vier Fälle über den charakteristischen Verlauf einer Funktion kennen gelernt.
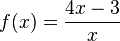
Diese Vermutung lässt sich mathematisch untersuchen, wobei es hier hilfreich ist, f als Differenz zu schreiben. f (x) =
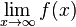 sprich"Limes von f (x) für x gegen + 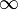 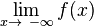 wird untersucht, wie sich f (x) für immer kleiner werdende x- Werte verhält.
|
AllgemeinIm Applet siehst du die gebrochen rationale Funktion Über die Schieberegler a und b lässt sich der Graph der Funktion verändern. Betrachte auch hier das Verhalten der Funktion für x gegen + oder -
Allgemein gilt: Auf gleiche Weise definiert man den Grenzwert einer Funktion f für immer kleiner werdende x- Werte, also für x gegen - Die Gerade y = G ist dann eine waagrechte Asymptote für den Graphen von f. Nähert sich eine Funktion f für immer größere x- Werte keiner festen Grenze an, sondern fällt bspw. gegen
Stimmt der Grenzwert einer Funktion für |
ÜbungOrdne den Funktionsgraphen den richtigen Grenzwert zu.
Manipulationen an Funktionen |
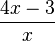 scheint sich für immer größer werdende x- Werte der Gerade
scheint sich für immer größer werdende x- Werte der Gerade 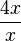 -
-  =
= 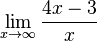 =
= 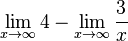 =
= 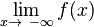 =
= 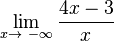 =
= 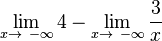 =
= 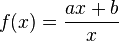
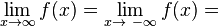
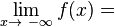
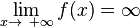
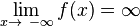 und
und 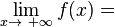
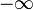 , so heißt f divergent und man schreibt:
, so heißt f divergent und man schreibt: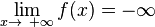 .
.
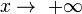 mit dem Grenzwert für
mit dem Grenzwert für  überein, lassen sich beide Grenzwerte auch zusammenfassen, wie es in der folgenden Übung gemacht wurde.
überein, lassen sich beide Grenzwerte auch zusammenfassen, wie es in der folgenden Übung gemacht wurde.

