Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).KW 39: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 74: | Zeile 74: | ||
|'''f)''' | |'''f)''' | ||
| <math>\sqrt{u^3v^3}</math> | | <math>\sqrt{u^3v^3}</math> | ||
| + | |} | ||
| + | <br /> | ||
| + | <br /> | ||
| + | ====<span style="color:green">Aufgabe III</span>==== | ||
| + | Mache den Nenner rational, vereinfache und gib, wenn nötig, einschränkende Bedingungen an. | ||
| + | {| | ||
| + | ! style="width:2.5em" | | ||
| + | ! style="width:15em" | | ||
| + | ! style="width:2.5em"| | ||
| + | ! style="width:15em" | | ||
| + | |- | ||
| + | |'''a)''' | ||
| + | | <math>\frac{1}{\sqrt{5}}</math> | ||
| + | |'''b)''' | ||
| + | | <math>\frac{5}{\sqrt{a}}</math> | ||
| + | |- | ||
| + | |'''c)''' | ||
| + | | <math>\frac{\sqrt{b}}{\sqrt{b+d}}</math> | ||
| + | |'''d)''' | ||
| + | | <math>\frac{2}{5\sqrt{z}}</math> | ||
|} | |} | ||
Version vom 30. September 2018, 20:38 Uhr
Inhaltsverzeichnis |
Wochenplan KW 39
Besprechung Mi 10.10.
- grüne Aufgaben sind Pflichtaufgaben
- orange Aufgaben sind optional zur vertiefenden Übung
- Abgabe der Hausaufgabe bis Montag 08.10. um 18:00 Uhr
Aufgabe I
Berechne oder vereinfache.
| a) | 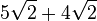
|
b) | 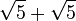
|
| c) | 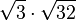
|
d) | 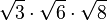
|
| e) | 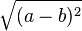
|
f) | 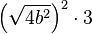
|
| g) | 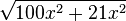
|
h) | 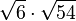
|
| i) | 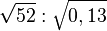
|
j) | 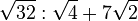
|
| k) | 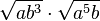
|
l) | 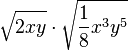
|
| m) | 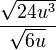
|
n) | 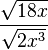
|
Aufgabe II
Radiziere teilweise.
| a) | 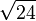
|
b) | 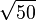
|
| c) | 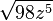
|
d) | 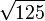
|
| e) | 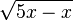
|
f) | 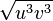
|
Aufgabe III
Mache den Nenner rational, vereinfache und gib, wenn nötig, einschränkende Bedingungen an.
| a) | 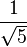
|
b) | 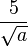
|
| c) | 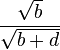
|
d) | 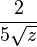
|

