Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Graphisches Ableiten: Unterschied zwischen den Versionen
| Zeile 30: | Zeile 30: | ||
== Aufgabe 3 (Förder- & Forderaufgabe) == | == Aufgabe 3 (Förder- & Forderaufgabe) == | ||
| + | |||
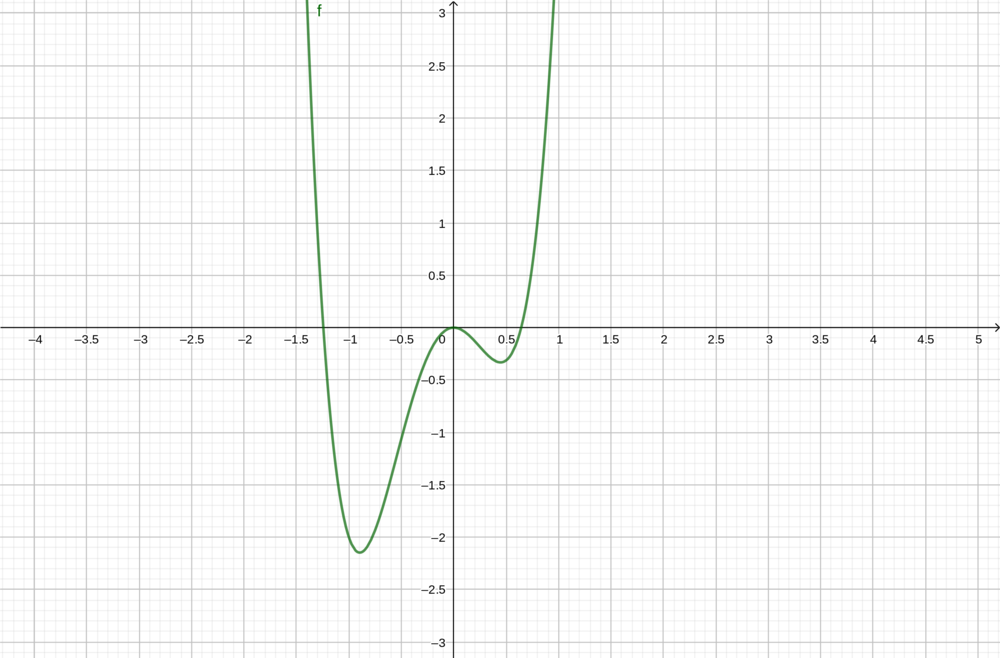
| + | Die Abbildung zeigt den Graphen einer Funktion f(x). Welche Annahmen kannst du über f'(x) treffen? | ||
| + | Beantworte die Fragen. | ||
[[Datei:Aufgabe 3.png|f(x)=5x^(4)+3x^(3)-4x^(2)|1000px|links|rahmenlos]]<br /> | [[Datei:Aufgabe 3.png|f(x)=5x^(4)+3x^(3)-4x^(2)|1000px|links|rahmenlos]]<br /> | ||
Version vom 14. Oktober 2018, 17:20 Uhr
Bei einer Kurvendiskussion werden markante Punkte gesucht, die uns Auskunft über die Eigenschaften einer Funktion geben. Das wichtigste Hilfsmittel ist dabei die Ableitung. Kenntnisse über den Zusammenhang einer Funktion und ihrer Ableitung sind daher grundlegend für die Analysis. In diesem Lernpfad kannst du üben, Funktionen und ihre Ableitungen anhand ihrer Graphen zu untersuchen. Im Folgenden findest du Aufgaben um deine Kenntnisse im graphischen Ableiten zu vertiefen (Forderaufgaben) aber auch um Lücken zu schließen und Stoff zu wiederholen (Förderaufgaben). Unter jeder Aufgabe gibt es Hilfestellungen, auf die du zurückgreifen kannst, wenn du mal nicht weiterkommst.
- Wenn dir das Thema noch Schwierigkeiten bereitet, beginne mit den Förderaufgaben (Aufgabe 1 bis Aufgabe 3).
- Wenn du dich bereits sicher fühlst, probiere die Forderaufgaben (Aufgabe 3 Aufgabe 5).
Inhaltsverzeichnis |
Aufgabe 1 (Förderaufgabe)
Ordne den Graphen der Funktionen f(x) die richtigen Ableitungen zu.
Aufgabe 2 (Förderaufgabe)
Aufgabe 3 (Förder- & Forderaufgabe)
Die Abbildung zeigt den Graphen einer Funktion f(x). Welche Annahmen kannst du über f'(x) treffen? Beantworte die Fragen.
Aufgabe 4 (Forderaufgabe)
Die Abbildung zeigt den Graphen einer Funktion f'(x). Skizziere die dazugehörige Funktion f(x) in deinem Heft und erkläre dein Vorgehen.