Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Teresa WWU3/Test: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
=Die Steigung eines Funktionsgraphen in einem Punkt= | =Die Steigung eines Funktionsgraphen in einem Punkt= | ||
| + | |||
| + | <div style="margin:0; margin | ||
| + | -right:3px; margin | ||
| + | -left:3px; border:3px solid #FF7F00; padding: 1em 1em | ||
| + | 1em 1em; background-color:#C6E2FF; align:left;"> <center><table border="0" width="750px | ||
| + | " | ||
| + | cellpadding=5 cellspacing=15> <tr><td width="300px" valign="top"> | ||
| + | Dieser Lernpfad beschäftigt sich mit der '''Steigung eines Funktionsgraphen in einem Punkt.''' | ||
| + | |||
| + | In den '''Aufgaben 1 und 2''' wird die grundlegende Vorstellung von Sekante und Tangente behandelt. | ||
| + | |||
| + | In den '''Aufgaben 3, 4 und 5''' geht es darum Tangentengleichungen und Normalengleichungen aufzustellen. | ||
| + | |||
| + | '''Aufgabe 6''' behandelt den Zusammenhang der Steigung und der Ableitung in einem Punkt. | ||
| + | |||
| + | (Aufgaben 7 und 8) | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
==Lückentexte zu Tangente und Sekante== | ==Lückentexte zu Tangente und Sekante== | ||
{{Aufgaben|1| | {{Aufgaben|1| | ||
Version vom 24. Oktober 2018, 18:12 Uhr
Inhaltsverzeichnis |
Die Steigung eines Funktionsgraphen in einem Punkt
|
Dieser Lernpfad beschäftigt sich mit der Steigung eines Funktionsgraphen in einem Punkt. In den Aufgaben 1 und 2 wird die grundlegende Vorstellung von Sekante und Tangente behandelt. In den Aufgaben 3, 4 und 5 geht es darum Tangentengleichungen und Normalengleichungen aufzustellen. Aufgabe 6 behandelt den Zusammenhang der Steigung und der Ableitung in einem Punkt. (Aufgaben 7 und 8) |
Lückentexte zu Tangente und Sekante
|
|
|
In diesem Applet siehst du den Graphen einer Funktion f und eine Gerade a. Weiterhin findest du in der rechten oberen Ecke zwei Regler, an denen du x0 und h einstellen kannst. Was fällt dir in Hinblick auf die Gerade a auf, wenn du den Regler von h verstellst? Fülle dazu den unter dem Applet stehenden Lückentext aus.
Benötigst du einen Tipp? Dann klicke auf die Glühbirne in der oberen linken Ecke des Lückentextes. Verwende für das Ausfüllen der Lücken bitte die folgende Schreibweise für Koordinaten: "(x/y)".
|
Tangentengleichung aufstellen
|
|
|
a)
Bestimme die Gleichung der Tangente an die Funktion b)
In welchem Punkt berührt die Tangente |
|
|
Ableitung und Steigung
|
Schaue dir das Applet an und entscheide auf Grundlage dessen, ob die unten stehenden Aussagen richtig oder falsch sind. Hinweis: Du kannst den Punkt P und auch die damit verbundene Tangente t mit deiner Maus bewegen, um dir die Aussagen zu veranschaulichen.
|
Forderaufgaben
|
In der Abbildung siehst du eine Funktion, sowie eine Tangente dieser Funktion im Punkt A. Mit dem Schieberegler kannst du an der markierten Stelle ran- und rauszoomen. Auf der rechten Seite der Abbildung siehst du alles vergrößert. Probiere zunächst aus, was passiert wenn du ganz nah reinzoomst und den Ausschnitt so weit es geht vergrößerst. Bewerte folgende Aussage "Wenn man sehr nah rangeht, stimmt die Funktion an der Stelle A mit der Tangente überein". Was hast du gesehen? Stimmst du zu? Wenn ja, warum? |
|
In der untenstehenden Grafik siehst du eine Funktion, sowie deren Punkte P und Q. Bei P und Q ist jeweils eine Tangente an die Funktion angelegt, erkennnbar durch die rot gestrichelten Linien.Die beiden Punkte lassen sich verschieben. a) Bestimme mithilfe der Abbildung die Ableitung der Funktion im Punkt P.
Versuche nachzuvollziehen was Lisa meint, indem du wie sie die Punkte verschiebst. Findest du auch zwei Tangenten? Kann es überhaupt zwei Tangenten in einem Punkt geben? Wie würdest du Lisas Frage beantworten: Was bedeutet das für die Ableitung in diesem Punkt? und für die Ableitung der Funktion?
|
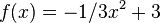 im Punkt
im Punkt 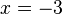 .
.
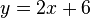 .
.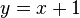 den Graphen
den Graphen 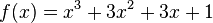 ?
?
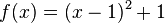 so, dass die Tangente (g) senkrecht zur Tangente (a) an der Stelle 1,25 (Punkt A) ist.
so, dass die Tangente (g) senkrecht zur Tangente (a) an der Stelle 1,25 (Punkt A) ist.
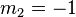 gilt, so stehen die Geraden senkrecht aufeinander. (Mit
gilt, so stehen die Geraden senkrecht aufeinander. (Mit 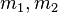 sind die beiden Steigungen der Geraden gemeint.)
sind die beiden Steigungen der Geraden gemeint.)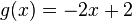 .
.
