Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Die Steigung eines Funktionsgraphen in einem Punkt: Unterschied zwischen den Versionen
| Zeile 107: | Zeile 107: | ||
''Hinweis: Du kannst den Punkt P und auch die damit verbundene Tangente t selbst bewegen, um dir die Aussagen zu veranschaulichen. Oder du nutzt alternativ den eingebauten Regler.'' | ''Hinweis: Du kannst den Punkt P und auch die damit verbundene Tangente t selbst bewegen, um dir die Aussagen zu veranschaulichen. Oder du nutzt alternativ den eingebauten Regler.'' | ||
| − | <iframe scrolling="no" title="Lernpfad 1" src="https://www.geogebra.org/material/iframe/id/vrcchyux/width/1522/height/585/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width=" | + | <iframe scrolling="no" title="Lernpfad 1" src="https://www.geogebra.org/material/iframe/id/vrcchyux/width/1522/height/585/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="950px" height="350px" style="border:0px;"> </iframe> |
<iframe src="https://learningapps.org/watch?v=pwhjkhu0j18" style="border:0px;width:70%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pwhjkhu0j18" style="border:0px;width:70%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
Version vom 28. November 2018, 20:22 Uhr
|
Dieser Lernpfad beschäftigt sich mit der Steigung eines Funktionsgraphen in einem Punkt. In den Aufgaben 1 und 2 wird die grundlegende Vorstellung von Sekanten und Tangenten behandelt. In den Aufgaben 3, 4 und 5 geht es darum Tangentengleichungen und Normalengleichungen aufzustellen. Aufgabe 6 behandelt den Zusammenhang der Steigung und der Ableitung in einem Punkt. Bei den Aufgaben 7 und 8 handelt es sich um Forderaufgaben im Bereich lokale Linearität und Ableitung in besonderen Punkten. |
Inhaltsverzeichnis |
Unterscheidung Tangente und Sekante
|
|
|
In diesem Applet siehst du den Graphen einer Funktion f und eine Gerade a. Weiterhin findest du in diesem zwei Regler, an denen du x0 und h einstellen kannst.
Hinweis: Beachte hier, dass die Dezimalzahlen mit Punkt und nicht wie gewohnt mit Komma geschrieben werden. Verwende für das Ausfüllen der Lücken bitte die folgende Schreibweise für Koordinaten: "(x/y)".
|
Tangentengleichungen aufstellen
|
Die Tangente an die Funktion
|
|
Bestimme die Gleichung der Tangente an die Funktion
|
|
|
|
Schaue dir das Applet an und entscheide auf Grundlage dessen, ob die unten stehenden Aussagen richtig oder falsch sind. Hinweis: Du kannst den Punkt P und auch die damit verbundene Tangente t selbst bewegen, um dir die Aussagen zu veranschaulichen. Oder du nutzt alternativ den eingebauten Regler.
|
Forderaufgaben
|
In der Abbildung siehst du eine Funktion, sowie eine Tangente dieser Funktion im Punkt A. Mit dem Schieberegler kannst du an der markierten Stelle ran- und rauszoomen. Der rot markierte Ausschnitt ist auf der rechten Seite der Abbildung vergrößert dargestellt. Probiere zunächst aus, was passiert, wenn du ganz nah reinzoomst und den Ausschnitt so weit es geht vergrößerst. Bewerte folgende Aussage: "Wenn man sehr stark zoomt, stimmt die Funktion an der Stelle A mit der Tangente überein". Was hast du gesehen? Stimmst du zu? Wenn ja, warum? Halte deine Überlegungen stichpunktartig fest und überprüfe diese anschließend anhand der unten stehenden Lösung. |
|
In der untenstehenden Grafik siehst du den Graph einer Funktion, sowie deren Punkt P. Bei P ist eine Tangente an die Funktion angelegt, erkennbar durch die rot gestrichelten Linien. Der Punkt lässt sich verschieben. Mithilfe des Buttons oben rechts im Applet lässt sich der Punkt zur ursprünglichen Position zurücksetzen. a) Bestimme mithilfe der Abbildung durch genaues Hinsehen die Ableitung der Funktion im Punkt P.
Versuche nachzuvollziehen was Lisa meint, indem du wie sie den Punkt P verschiebst. Kann das überhaupt sein? Wie würdest du Lisas Frage beantworten?
|
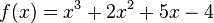 im Punkt
im Punkt 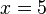 soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.
soll berechnet werden. Im folgenden Applet siehst du die dazu vorgenommenen Rechenschritte und Anweisungen.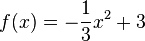 im Punkt
im Punkt 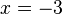 .
.
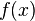 ist
ist 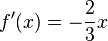 .
.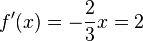 .
.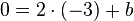 , also
, also 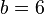 .
.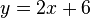 .
.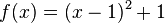 so, dass die Tangente g senkrecht zur Tangente a an der Stelle 1,25 (Punkt A) ist. Notiere deine einzelnen Rechenschritte in deinem Heft.
so, dass die Tangente g senkrecht zur Tangente a an der Stelle 1,25 (Punkt A) ist. Notiere deine einzelnen Rechenschritte in deinem Heft.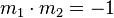 gilt, so stehen die Geraden senkrecht aufeinander. (Mit
gilt, so stehen die Geraden senkrecht aufeinander. (Mit 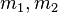 sind die beiden Steigungen der Geraden gemeint.)
sind die beiden Steigungen der Geraden gemeint.)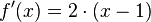
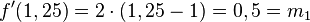
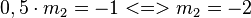
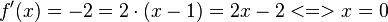
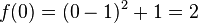 , also
, also 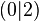
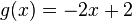 .
.
