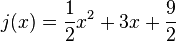Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).KW 50: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 49: | Zeile 49: | ||
Beschreibe außerdem, wie die Parabel aus der Normalparabel hervorgeht. | Beschreibe außerdem, wie die Parabel aus der Normalparabel hervorgeht. | ||
:a) <math>f(x)=x^2+3x+4</math> | :a) <math>f(x)=x^2+3x+4</math> | ||
| − | :b) <math>x^2-4x+4</math> | + | :b) <math>g(x)=x^2-4x+4</math> |
| − | :c) <math>2x^2-4x-6</math> | + | :c) <math>h(x)=2x^2-4x-6</math> |
| − | :d) <math>-x^2-x+5</math> | + | :d) <math>i(x)=-x^2-x+5</math> |
| + | :e) <math>j(x)=\frac{1}{2}x^2+3x+\frac{9}{2}</math> | ||
Version vom 10. Dezember 2018, 17:32 Uhr
Inhaltsverzeichnis |
Wochenplan KW 50
Besprechung Mi 19.12.
- grüne Aufgaben sind Pflichtaufgaben
- orange Aufgaben sind optional zur vertiefenden Übung
- Abgabe der Hausaufgabe bis Montag 17.12. um 18:00 Uhr im Notizbuch.
Aufgabe I
Gib an, ob die Parabel zu der gegebenen Gleichung nach oben bzw. nach unten geöffnet ist und ob sie enger ist oder weiter als die Normalparabel.
| a) | 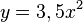
|
b) | 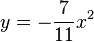
|
| c) | 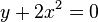
|
d) | 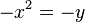
|
| e) | 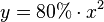
|
f) | 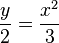
|
Aufgabe II
Bestimme jeweils einen möglichen Funktionsterm, der auf die gegebenen Eigenschaften zutrifft.
- a) Der Graph ist eine Normalparabel, die um zwei Einheiten nach oben und um drei Einheiten nach rechts verschoben ist.
- b) Der Graph ist enger als die Normalparabel und die y-Koordinate des Scheitels liegt bei 2.
- c) Der Graph aus b) gespiegelt an der x-Achse.
- d) Der Graph ist weiter als die Normalparabel und die x-Koordinate des Scheitels liegt bei 3.
- e) Der Graph aus d) gespiegelt an der y-Achse.
- f) Der Scheitel S der Parabel liegt bei S(2|3) und die Parabel ist nach unten geöffnet.
- g) Der Graph aus f) gespiegelt an der x- und y-Achse.
Aufgabe III
Gib den Scheitel folgender Funktionen an. Forme dazu die gegebenen Funktionsterme in Scheitelform um.
Beschreibe außerdem, wie die Parabel aus der Normalparabel hervorgeht.
- a)
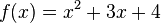
- b)
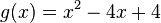
- c)
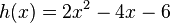
- d)
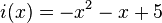
- e)