Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Verhalten nahe 0: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| Zeile 2: | Zeile 2: | ||
<popup Name="Tipp">Bsp. Schreibweise: Die Funktion <math>f(x)=x^4+x-1</math> hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie <math>g(x)=x^4</math>. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.</popup> | <popup Name="Tipp">Bsp. Schreibweise: Die Funktion <math>f(x)=x^4+x-1</math> hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie <math>g(x)=x^4</math>. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.</popup> | ||
| + | }} | ||
{{Aufgaben|2|Gegeben ist die Funktion f mit <math>f(x)=1/6 x^4-4/3x^2-3/2</math>. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.}} | {{Aufgaben|2|Gegeben ist die Funktion f mit <math>f(x)=1/6 x^4-4/3x^2-3/2</math>. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.}} | ||
Version vom 6. November 2019, 10:08 Uhr
|
|
|
Gegeben ist die Funktion f mit |
|
Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0. a)
b)
c)
|
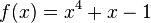 hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie
hat als höchsten Exponenten 4, verhält sich also gegen Unendlich wie 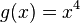 . Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.
. Also geht sie für x gegen - Unendlich gegen + Unendlich und für x gegen + Unendlich auch gegen + Unendlich.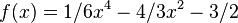 . Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
. Untersucht das Verhalten des Graphen für x gegen Unendlich und für x nahe 0.
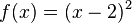
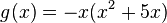
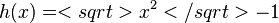
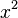 , also Fehler beim Parsen(Lexikalischer Fehler): x--> -∞ = ∞
, also Fehler beim Parsen(Lexikalischer Fehler): x--> -∞ = ∞

