Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Trigonometrische Funktionen: Unterschied zwischen den Versionen
K (→Die Winkelfunktionen am Einheitskreis) |
K (→Die Winkelfunktionen am Einheitskreis) |
||
| Zeile 13: | Zeile 13: | ||
<math>\cos (\alpha) =\frac{Ankathete}{Hypothenuse} = \frac{Ankathete}{1} = Ankathete </math> | <math>\cos (\alpha) =\frac{Ankathete}{Hypothenuse} = \frac{Ankathete}{1} = Ankathete </math> | ||
<br> <br> | <br> <br> | ||
| − | Der Punkt P hat also die Koordinaten | + | Der Punkt P hat also die Koordinaten <math>P(\cos (\alpha ) /\sin (\alpha ))</math>. |
Diese Bezeichnung gilt auch für Winkel größer als 90°. Je nachdem, in welchem Quadranten des Koordinatensystems P liegt, sind die Werte für <math>\cos (\alpha) </math> bzw. <math>\sin (\alpha) </math> unter Umständen auch negativ. | Diese Bezeichnung gilt auch für Winkel größer als 90°. Je nachdem, in welchem Quadranten des Koordinatensystems P liegt, sind die Werte für <math>\cos (\alpha) </math> bzw. <math>\sin (\alpha) </math> unter Umständen auch negativ. | ||
Version vom 7. Januar 2023, 22:57 Uhr
Inhaltsverzeichnis |
Die Winkelfunktionen am Einheitskreis
Sinus und Kosinuns waren zunächst nur für Winkel zwischen 0° und 90° definiert.
Die Erweiterung dieser Definitionen ergibt sich, wenn 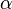 als Drehwinkel am Einheitskreis betrachtet wird.
als Drehwinkel am Einheitskreis betrachtet wird.
Im Applet sind der Sinus und Kosinuns am Einheitskreis dargestellt.
Der Einheitskreis hat den Radius 1, auf der Kreislinie befindet sich ein Punkt P (der im Applet auf der Krteislinie bewegt werden kann). Stelle dir einen Zeiger 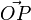 vor, der sich gegen den Uhrzeigersinn dreht. Zu jeder Stellung des Zeigers gehören ein Winkel
vor, der sich gegen den Uhrzeigersinn dreht. Zu jeder Stellung des Zeigers gehören ein Winkel 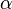 und ein rechtwinkliges Dreieck mit der Hypothenusenlänge 1 (Hypothenuse = Radius). Da die Hypothenuse die Länge 1 hat, gilt:
und ein rechtwinkliges Dreieck mit der Hypothenusenlänge 1 (Hypothenuse = Radius). Da die Hypothenuse die Länge 1 hat, gilt:
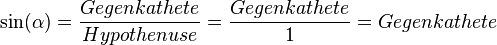
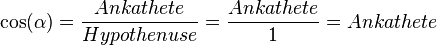
Der Punkt P hat also die Koordinaten 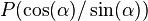 .
Diese Bezeichnung gilt auch für Winkel größer als 90°. Je nachdem, in welchem Quadranten des Koordinatensystems P liegt, sind die Werte für
.
Diese Bezeichnung gilt auch für Winkel größer als 90°. Je nachdem, in welchem Quadranten des Koordinatensystems P liegt, sind die Werte für 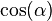 bzw.
bzw. 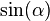 unter Umständen auch negativ.
unter Umständen auch negativ.
Das Bogenmaß
Eine andere Möglichkeit, den Winkel und damit P anzugeben, ist das sogenannte Bogenmaß. Als Bogenmaß wird die Länge x des Bogens bezeichnet, den der Zeiger bis zum Punkt P entlang läuft. Die Einheit des Bogenmaßes lautet rad (= Radiant), wird in der Regel aber weggelassen.
Bild einfügen: Einheitskreis Bogenmaß
Für einen ganzen Kreis beträgt das Gradmaß 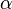 = 360° und das Bogenmaß x = 2
= 360° und das Bogenmaß x = 2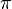 (der Umfang des Einheitskreises beträgt
(der Umfang des Einheitskreises beträgt 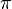 ). Die genaue Formel zur Umrechnung eines Winkels im Gradmaß in das Bogenmaß findest du unten im Definitionskasten.
). Die genaue Formel zur Umrechnung eines Winkels im Gradmaß in das Bogenmaß findest du unten im Definitionskasten.
Die Sinusfunktion und Kosinusfunktion
Man kann nun die Sinusfunktion betrachten, die jedem Winkel (gemessen im Gradmaß oder - üblicherweise - im Bogenmaß) den sinuswert des Winkels zuordnet. Ebenso wird die Kosinusfunktion definiert, die jedem Winkel den Kosinuns des Wikels zuordnet. Im Applet kannst du die Definition der Sinusfunktion am Einheitskreis nachvollziehen, im zweiten Applet die Definition der Kosinusfunktion. Du kannst dabei jeweils den Punkt K auf dem Einheitskreis bewegen.
|
Definition
Mithilfe des Einheitskreises kann man die Defintion von Sinus und Kosinus auf Winkel größer als 90° erweitern. Zu jedem Winkel |
Dabei ist man nicht darauf beschränkt, Winkel zwischen 0° und 360° zu betrachten. Man kann den Kreis auch mehrfach umlaufen, oder auch den Punkt den Kreis in der anderen Richtung durchlaufen lassen und somit Sinuswerte von negativen Winkel betrachten. Probiere dies im Applet
aus.
|
Untersuche mit Hilfe des Applets die Sinusfunktion hinsichtlich ihrer folgenden Eigenschaften und notiere die Ergebnisse im Heft:
|
Zu einem Funktionswert der Sinusfunktion können mehrere Winkel gehören, die den gleichen Sinuswert haben. Verändere hierzu im Applet den Wert von a und suche alle Winkel x, für die 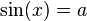 gilt.
gilt.
Hausaufgabe: Bearbeite die Aufgaben 9 und 10 auf Seite 137 im Buch.
Tranformationen der Funktionen
Aus dem Alltag sind dir vielleicht verschiedende Arten von grafischen Darstellungen bekannt, die ähnlich aussehen wie die Sinuskurve, z. B. bei der Darstellung von Schwingungen, wie sie bei der Aufzeichnung von Wechselspannungen am Oszilloskop im Physiksaal oder bei der Darstellung von Ebbe und Flut auftauchen. Die Gesetzmäßigkeiten, die diesen Schwingungen zugrunde liegen, lassen sich tatsächlich oftmals mithilfe von Gleichungen beschreiben, in denen Sinusfunktionen vorkommen. Die sogenannte "Grundfunktion" 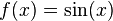 allein reicht dazu allerdings nicht aus; sie muss zur Modellierung dieser Funktionen auf verschiedene Arten transformiert werden. Mit diesen Transformationen sollst du dich nun näher beschäftigen:
allein reicht dazu allerdings nicht aus; sie muss zur Modellierung dieser Funktionen auf verschiedene Arten transformiert werden. Mit diesen Transformationen sollst du dich nun näher beschäftigen:
Verschiedene Transformationsarten (d. h. das Strecken bzw. Stauchen, das Verschieben sowie das Spiegeln von Graphen) sind dir bereits von den quadratischen Funktionen, Potenzfunkionen und Exponentialfunktionen bekannt.
Die allgemeine Sinusfunktion hat die 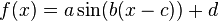 .
.
|
Untersuche mit Hilfe des Applets , welche Auswirkungen die Änderungen der Parameter a,b,c und d haben. Notiere die Ergebnisse in deinem Heft. Fertige auch geeignete Skizzen an. |
Ebenso kann man natürlich auch die allgemeine Kosinusfunktion 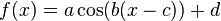 betrachten.
betrachten.
Zusatzaufgabe zur Ergänzung:
|
Untersuche mit Hilfe des Applets , welche Auswirkungen die Änderungen der Parameter a,b,c und d haben. Notiere die Ergebnisse in deinem Heft. Fertige auch geeignete Skizzen an. |
Nun soll noch ein Zusammenhang zwischen der Sinus- und Kosinusfunktion untersucht werden.
|
Untersuche mit Hilfe des Applets , wie die Kosinusfunktion aus der Sinusfunktion hervorgeht. Erkläre. |
Funktionsgleichungen bestimmen
Nun sollen die Parameter zu gegebenen Graphen bestimmt werden.
|
Bearbeite dazu die Aufgaben auf den folgenden Seiten: |
Weitere Übungsaufgaben:
|
Bearbeite die Aufgaben auf den folgenden Seiten. Mit dem Schieberegler kannst du die Lösung schrittweise einblenden. |
Anwendungen
Auf der Seite Anwendungen werden noch ein paar Anwendungen betrachtet.
Hinweis: auf der Seite wird als allgemeine Sinusfunktion 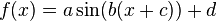 verwendet. Der Parameter c hat also ein anderes Vorzeichen. Die gewonnene Funktionsvorschrift ist aber auf jeden Fall die gleiche, auch wenn man mit der allgemeinen Sinusfunktion
verwendet. Der Parameter c hat also ein anderes Vorzeichen. Die gewonnene Funktionsvorschrift ist aber auf jeden Fall die gleiche, auch wenn man mit der allgemeinen Sinusfunktion 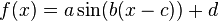 arbeitet wie wir.
arbeitet wie wir.
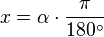 .
Die Funktion
.
Die Funktion 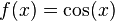 Kosinusfunktion.
Kosinusfunktion.

