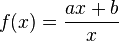Grenzwerte im Unendlichen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
|
Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält.
Anschaulich gesprochen: Man betrachtet den Funktionsgraphen am rechen und linken Bildrand.
Bei ganzrationalen Funktionen hast du bereits vier Fälle über den charakteristischen Verlauf einer Funktion kennen gelernt.
Auch mit dem Verhalten von gebrochen rationalen Funktionen für immer größer werdende x- Werte hast du dich schon auseinandergesetzt.
Dieses Wissen wird jetzt noch weiter vertieft.
Hierfür ein Beispiel: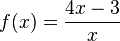
|
|
- Fülle die Wertetabelle vollständig aus, indem du die Funktionswerte in das jeweilige Feld eingibst. Wenn sich das Feld grün färbt, war deine Eingabe richtig.
- Übertrage die berechneten Punkte in das GeoGebra-Applet und skizziere den Verlauf des Funktionsgraphen von f über den Button "Freihandskizze erkennen".
- Wie verhält sich die Funktion f für immer größer, bzw. immer kleiner werdende x- Werte?
- Über die beiden Kontrollkästchen lässt sich der Graph der Funktion f und die Gerade, an die sich f annähert, anzeigen.
- Mit dem letzten Symbol "Verschiebe Zeichenblatt" in der Werkzeugleiste kannst du dir die beiden Graphen auch über den eigentlichen Bildrand hinweg anschauen.
- Unter dem gleichen Symbol lässt sich auch das Werkzeug "Vergrößere" auswählen.
Sieh dir genau an, ob sich die beiden Graphen berühren!
|
Diese Vermutung lässt sich mathematisch untersuchen:
f (x) = 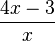 = = 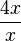 - -  = 4 - = 4 - 
Für immer größer werdende x- Werte wird der Bruch  immer kleiner, nähert sich also der Null an, während die Zahl 4 unverändert bleibt. immer kleiner, nähert sich also der Null an, während die Zahl 4 unverändert bleibt.
Also nähert sich f (x) für immer größer werdende x- Werte immer mehr 4 - 0 = 4 an.
Die Betrachtung einer Funktion f unter immer größer werdenden x- Werten schreibt man mathematisch:
Limes von f (x) für x gegen + 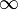 : :
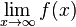
Durch den Limes von f für x gegen - 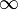
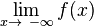
wird untersucht, wie sich f (x) für immer kleiner werdende x- Werte verhält.
In unserem Beispiel können wir schreiben:
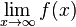 = = 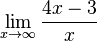 = = 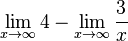 = 4 - 0 = 4 = 4 - 0 = 4
Das gleiche Ergebnis erhält man, wenn man den Limes von f für x gegen - 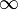 untersucht, da das Vorzeichen hier keine Rolle spielt. untersucht, da das Vorzeichen hier keine Rolle spielt.
Damit heißt 4 der Grenzwert der Funktion f für x gegen + 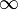 und gegen - und gegen - 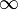 . .
|
Allgemein
Im Applet siehst du die gebrochen rationale Funktion 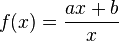 . .
Über die Schieberegler a und b lässt sich der Graph der Funktion verändern.
Welchen Zusammenhang kannst du zwischen a, b und der waagrechten Asymptote von f feststellen?
Im nächsten Applet ist die Funktion f(x) = a ∙ eb ∙ x + c abgebildet.
Welcher Zusammenhang besteht hier zwischen den drei veränderlichen Zahlen a, b und c und der waagrechten Asymptote von f?
|
Übung
Manipulationen an Funktionen
|
|
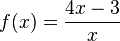
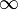 :
: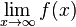
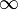
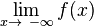
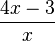 scheint sich für immer größer werdende x- Werte der Gerade
scheint sich für immer größer werdende x- Werte der Gerade 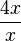 -
-  =
= 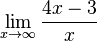 =
= 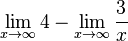 =
=