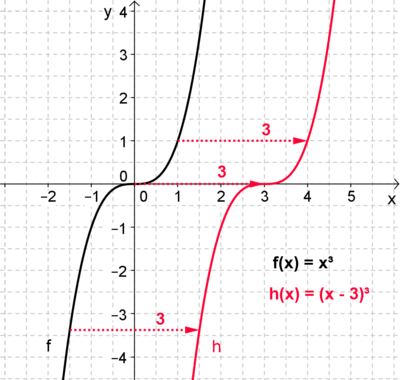
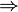Verschiebung in x- Richtung
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
|
Fülle den ersten Abschnitt auf deinem Arbeitsblatt aus:
Achte dabei darauf, dass die Gleichungen immer mathematisch richtig bleiben!
|
|
Vergleiche die beiden Graphen an den vorgegebenen Werten:
- h(1,5) = -3,375 = f (-1,5) = f (1,5 - ____)
- h(3) = _____ = f (___) = f (_____ - _____)
- h(4) = ____________________________________
Wie lässt sich h(x) aus f (x) herleiten?
 h(x) = ____________________________________ h(x) = ____________________________________
Für jeden x - Wert ist der Funktionswert von h gleich dem Funktionswert von f an der Stelle __________.
|
Vergleiche deine Antworten mit der Lösung und bessere gegebenenfalls aus:
Übertrage auch die Pfeillängen und den Funktionsterm von h(x) in das Bild.
|
Allgemein
Im folgenden Applet ist die ganzrationale Funktion f: x -> x3 abgebildet.
Verschiebe den Graphen der Funktion h: x -> (x - a)3, indem du über den Schieberegler den Parameter a veränderst.
Welche Auswirkungen hat eine Veränderung von a auf den Graphen von h?
Was passiert, wenn a kleiner bzw. größer wird?
In welche Richtung wird der Graph von h verschoben, wenn a negativ bzw. positiv ist?
Vergleiche dazu die Wertetabelle!
Allgemein gilt:
Betrachtet man den Term f (x - a), wird der Graph von f um a Einheiten auf der x - Achse verschoben.
Für a < 0 wird der Graph nach links, für a > 0 nach rechts verschoben.
|
Übung
Hast du alles verstanden?
In dieser Übung kannst du dein Wissen noch einmal überprüfen:
Bestimme den Term des verschobenen Funktionsgraphen (bspw. in der Form x^2 + 1).
Der Term der ursprünglichen Funktion ist als Hilfe angegeben.
Manipulationen an Funktionen
|
|