Multiplikation von Brüchen

Das Rechnen mit Brüchen fällt vielen von uns schwer, weshalb ich im Folgenden das Berechnen von Brüchen bei einer Multiplikation, sowie Division erklären und erleichtern möchte.

Multiplikation von Brüchen:

Um euch effektiver helfen zu können, habe ich in diesem Video kurz erklärt, wie man richtig Brüche miteinander multipliziert→

Teste hier, ob du das Prinzip der Multiplikation von Brüchen verstanden hast:

Beim Multiplizieren von Brüche muss man Zähler mit Zähler und Nenner mit Nenner miteinander multiplizieren.

1.Aufgabe
Löse den Lückentext, indem du dein Wissen logisch anwendest.

Selin behauptet: "Wenn ich für ein Blech Muffins 1/3 Liter Milch brauche, dann brauche ich für 3 Bleche 3/9 Liter Milch." Selins Behauptung ist richtig und nicht falsch

2.Aufgabe
Berechne jeweils den Wert des Produktes.

  $\frac{1}{4}$   •   $\frac{6}{8}$   =   $\frac{6}{32}$    $\frac{2}{5}$   =   $\frac{4}{20}$   =   $\frac{1}{5}$  

		$\frac{6}{16}$
		$\frac{20}{28}$
		$\frac{5}{10}$

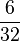
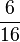
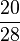
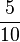
|width=5px| |valign="top" |

<div class="zuordnungs-quiz">

{| 
| <math>x \cdot\frac{6}{8}=\frac{3}{8}</math> |
| <math>\frac{1}{2} </math> |
| <math>\frac{6}{16} </math>  
|-
| <math>x\cdot\frac{1}{4}=\frac{5}{28}</math> |
| <math>\frac{5}{7} </math> |
|<math>\frac{20}{28} </math>
|-
| <math>x\cdot\frac{-2}{3}=\frac{-1}{3}</math> |
| <math>\frac{1}{2} </math> |
|<math>\frac{5}{10} </math>
|}

</div>

|}