Benutzer Diskussion:Jasmin WWU-2

 Herzlich Willkommen im Projektwiki - ein Wiki mit Schülern für Schüler.

• Bitte stelle Dich kurz auf Deiner Benutzerseite vor.
  • Bist Du Schüler/in (Studierende/r), dann nenne Deine Schule (Institution) und Deine Lehrkraft, in deren Unterricht Du das Projektwiki - ein Wiki mit Schülern für Schüler. nutzt.
  • Bist Du Lehrer/in (Lehrende/r), dann nenne Deine Schule (Institution) und/oder Unterrichtsfächer bzw. Kurse oder Projekte, in denen Du das Projektwiki - ein Wiki mit Schülern für Schüler. nutzt.
• Die wichtigsten Hilfen findest du unter: Kurzanleitung - Layout - Multimedia - Quiz - Tabellen
• Wenn du nicht mehr weiter weißt, helfen wir gerne weiter. Bitte stell deine Fragen bei einem Admin unter    Diskussion   . Unterschreibe deine Beiträge mit einem Klick auf das Symbol im WikiEditor unter "Erweitert".
• Bitte beachte die Richtlinien im Wiki.

Viel Spaß und eine gute Zusammenarbeit wünschen die Admins im Projektwiki - ein Wiki mit Schülern für Schüler.

-- New user message (Diskussion) 15:08, 6. Apr. 2018 (CEST)

Quadratische Funktionen

Scheitelpunktform und Normalform

Aufgabe 1

Merke Merksatz

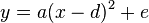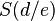Merke Terme quadratischer Funktionen können in der Form $y=a(x-d)^2+e$ angegeben werden (wobei a ≠ 0). Diese Darstellungsform nennt man Scheitelpunktform, da sich direkt aus dem Term der Scheitelpunkt ablesen lässt. Er hat die Koordinaten $S(d/e)$.