Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Von der mittleren zur lokalen Änderungsrate
Von der mittleren zur lokalen Änderungsrate
|
Infokästchen, dessen Text noch eingefügt werden muss |
|
Bestimmung von durchschnittlichen Änderungsraten |
1a Berechne die durchschnittliche Änderungsrate in den angegebenen Intervallen.
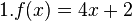 im Intervall
im Intervall ![[2,5]](/images/math/d/b/5/db5dc72ec1da78e609bf9f0ae1447688.png)
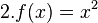 im Intervall
im Intervall ![[2,7]](/images/math/1/1/f/11fa16d050ab48b2dd318ff5b5817119.png)
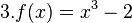 im Intervall
im Intervall ![[-2,1]](/images/math/7/0/1/7019f6fe0e7078b019e0586e7cbc564a.png)
1b) Dein Sportverein feiert dieses Jahr achtjähriges Bestehen. Zu diesem Anlass wird eine Tabelle mit den Mitgliederzahlen der letzten Jahre veröffentlicht:
| Jahr | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Anzahl der Mitglieder am Ende des Jahres | 210 | 336 | 351 | 371 | 342 | 365 | 387 | 411 |
Leider hat der Vorstand in seiner eigenen Schulzeit in Mathe nicht sehr gut aufgepasst und bittet dich, ihm bei der Beantwortung einiger Fragen zu helfen.
1) Wie viele Mitglieder sind seit Beginn der Mitgliedererfassung im Durchschnitt pro Jahr in deinem Verein hinzugekommen? Runde bitte auf zwei Nachkommastellen genau und überprüfe anschließend deine Lösung!
Seit Beginn der Mitgliedererfassung sind im Durchschnitt pro Jahr diese Anzahl an Mitgliedern zum Verein gekommen: (!25,13) (!22,30) (!31,74) (!2,23) (28,71)
2) Der aktuelle Vorstand arbeitet seit zwei Jahren zusammen. Sein Ziel war eine Steigerung der Mitglieder. Diese sollte im Mittel größer sein als der durchschnittliche Mitgliederzuwachs in den Jahren zuvor. Ist es Ihnen gelungen ihr Ziel zu erreichen?
Aufgabe 2: Unterscheidung der Änderungsraten
|
Ordne die verschiedenen Begriffe der richtigen Änderungsrate zu. |
|
Fertige in deinem Heft eine Tabelle zur durchschnittlichen und momentanen Änderungsrate mit den Begriffen aus Teilaufgabe a an. Stelle die zueinander passenden Begriffe gegenüber. |
|
Tim fährt mit dem Fahrrad zur Schule und muss an einer roten Ampel abbremsen. Für den in der Zeit t (in Sekunden) zurückgelegten Weg s(t) (in Meter) gilt:
(i) Berechne den zurückgelegten Weg nach 3 und 5 Sekunden. (ii) Berechne die Geschwindigkeit, die Tim in der Sekunde 3 bzw. in Sekunde 5 mit seinem Fahrrad fährt. (iii) Warum hat die oben genannte Formel im vorliegenden Sachzusammenhang für |
|
|
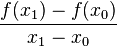 .
.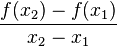 stellt den Differenzenquotienten dar. Der Differenzenquotient gibt die durchschnittliche Änderungsrate von f über dem Intervall [
stellt den Differenzenquotienten dar. Der Differenzenquotient gibt die durchschnittliche Änderungsrate von f über dem Intervall [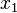 ;
;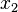 ] an.
] an.
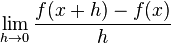 heißt Differentialquotient. Dieser Quotient ist anschaulich der Grenzwert der Sekantensteigung, wenn sich der Punkt
heißt Differentialquotient. Dieser Quotient ist anschaulich der Grenzwert der Sekantensteigung, wenn sich der Punkt 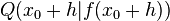 auf den Punkt P
auf den Punkt P 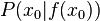 zu bewegt. Also ist es die Steigung der Tangente in P und entspricht der Ableitung in
zu bewegt. Also ist es die Steigung der Tangente in P und entspricht der Ableitung in 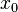 .
.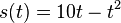 für
für ![t\in [0;5]](/images/math/d/1/7/d17e4f93b0be76b84d0dd79694840cff.png)
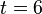 keinen Sinn?
keinen Sinn?

