Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Testseite
|
„Auf dieser Seite findest du Aufgaben, die dein Verständnis zum Sachkontext von Ableitungen vertiefen. Du wiederholst, in welchen Sachsituationen welche Rechnung benötigt werden. Ebenso wirst du vertiefen, welche mathematischen Ausdrücke auf welche Weise interpretiert werden. Die Aufgaben sind von leicht bis schwierig sortiert. Falls du dich schon sehr sicher fühlst, gibt es am Ende eine Bonusaufgabe.“ |
Inhaltsverzeichnis |
Aufgabe 1: Silvesterkracher
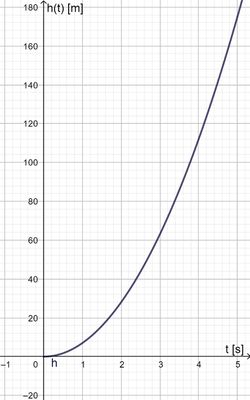
Die Höhe einer gezündeten Feuerwerksrakete kann in den ersten fünf Sekunden nach dem Start annähernd durch die Funktion 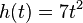 beschrieben werden (siehe Abbildung 1). Dabei wird die Zeit t nach dem Start in Sekunden und die Höhe h(t) in Metern angegeben. beschrieben werden (siehe Abbildung 1). Dabei wird die Zeit t nach dem Start in Sekunden und die Höhe h(t) in Metern angegeben. a) Bestimme zu den folgenden Termen die entsprechenden Werte
c) Wie groß ist die Beschleunigung des Feuerwerkskörpers drei Sekunden nach dem Start? |
Aufgabe 2: Aussagen der Ableitungsfunktion und Änderung der Einheiten
|
|
Spielwiese
=Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso sind andere Farben möglich, um etwas hervorzuheben.
Vorlagen
|
Tangente |
|
Sachzusammenhang |
|
Änderung |
30px Übung
Ableitungsregeln |
30px Merke
Differenzenquotient |
Dateien
Interaktive Applets
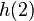
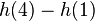
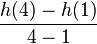
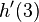
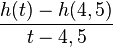 , für t → 4,5
, für t → 4,5