Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Mathematik 9a
Auf dieser Seite sollen quadratische Funktionen untersucht werden.
Inhaltsverzeichnis |
Einführung
Wir haben im Unterricht quadratische Funktionen der Form 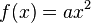 kennengelernt.
Dabei ist x die Variable, die alle Zahlen durchläuft. a ist ein Parameter und steht für einzelne Werte, die man einsetzt, und damit jeweils eine spezielle quadratische Funktion erhält. Für
kennengelernt.
Dabei ist x die Variable, die alle Zahlen durchläuft. a ist ein Parameter und steht für einzelne Werte, die man einsetzt, und damit jeweils eine spezielle quadratische Funktion erhält. Für 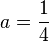 erhält man die Funktion
erhält man die Funktion 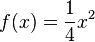 . Für
. Für 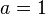 erhält man die einfachste quadratische Funktion
erhält man die einfachste quadratische Funktion 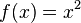 , deren Graph die Normalparabel ist.
, deren Graph die Normalparabel ist.
Im Folgenden soll untersucht werden, wie sich eine Veränderung des Parameters a auf den Graphen auswirkt.
Der Parameter a
Wir betrachten zunächst nur den Parameter a und untersuchen 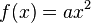 .
.
Im Applet ist zunächst a=1 gesetzt, also die Normalparabel eingezeichnet. Mit Hilfe des Schiebereglers kannst du den Parameter ändern.
|
a) Untersuche , was passiert, wenn du a änderst. |
Der Parameter c
Wir betrachten zunächst nun quadratische Funktionen der Form 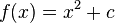 , wobei c wieder ein Parameter ist.
, wobei c wieder ein Parameter ist.
Im Applet
ist zunächst c=0 gesetzt, also die Normalparabel eingezeichnet.
Mit Hilfe des Schiebereglers kannst du den Parameter ändern.
|
a) Untersuche , was passiert, wenn du c änderst. |
Kombination
Im Applet kannst du beide Parameter ändern.
|
a) Für welchen Wert von a geht der Graph von |
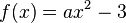 durch den Punkt
durch den Punkt 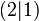 .
. 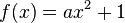 durch den Punkt
durch den Punkt 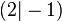 .
. 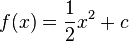 durch den Punkt
durch den Punkt 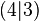 .
. 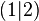 .
.
