Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Kehrsatz
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
< Gymnasium Untergriesbach | Klasse 7CD | Bereich 7C
Version vom 6. Juli 2018, 15:25 Uhr von Matthias Mohr (Diskussion | Beiträge)
Arbeitsaufträge:
- Schaue dir das Videos an, wie die Umkehrung des Satzes von Thales lautet.
- Beantworte die Kontrollfragen.
- Notiere dir, anhand der vorgegebenen Fragen, Bemerkungen in OneNote.
- Erstelle einen Hefteintrag in deinem Skript.
- Für Interessierte gibt es auch noch die Herleitung der Umkehrung des Satzes von Thales (Diese Aufgabe ist optional).
Inhaltsverzeichnis |
Kehrsatz zum Satz des Thales
Merke: Umkehrung des Satzes von Thales
Wenn ein Dreieck bei C einen rechten Winkel hat, dann liegt die Ecke C dieses Dreiecks auf dem Halbkreis über [AB].
Kontrollfragen
Für Interessierte: Beweis des Kehrsatzes (Optional)
Quellenangabe
Video "Rechtwinklige Dreiecke - Satz des Thales (Teil 1)" von Mathegym, über https://www.youtube.com/watch?v=RGZs_R7YFgE (Zugriff am 28.05.2018)
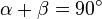 .
.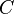 lässt sich daher eine Gerade
lässt sich daher eine Gerade 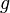 so legen, dass
so legen, dass 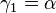
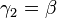
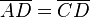 und
und 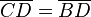 .
.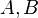 und
und 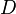 entfernt, liegen somit auf dem Kreis um
entfernt, liegen somit auf dem Kreis um ![[AB]](/images/math/5/e/3/5e32d4dbe98ef3af1b5123ccba43cbf7.png) ist.
ist.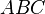 bei
bei