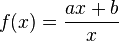Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Grenzwerte im Unendlichen: Unterschied zwischen den Versionen
| Zeile 56: | Zeile 56: | ||
<math>\lim_{x \to \infty}f (x)</math></center><br /> | <math>\lim_{x \to \infty}f (x)</math></center><br /> | ||
<br /> | <br /> | ||
| − | Durch den '''''Limes von f für x gegen '''<span style="color: red">-</span>''' <math>\infty</math>''''' wird untersucht, wie sich f (x) für immer '''<span style="color: red">kleiner</span>''' werdende x- Werte verhält. | + | Durch den '''''Limes von f für x gegen '''<span style="color: red">-</span>''' <math>\infty</math>'''''<br /> <center><math>\lim_{x\rightarrow\ -\infty} f(x)</math></center><br /> wird untersucht, wie sich f (x) für immer '''<span style="color: red">kleiner</span>''' werdende x- Werte verhält. |
In unserem Beispiel können wir schreiben:<br /> | In unserem Beispiel können wir schreiben:<br /> | ||
<br /> | <br /> | ||
| − | <math>\lim_{x \to \infty}f (x)</math> = <math>\lim_{x \to \infty}\frac{4x-3}{x}</math> = <math>\lim_{x \to \infty}4 - \lim_{x \to \infty}\frac{3}{x}</math> = 4 - 0 = 4<br /> | + | <math>\lim_{x \to \infty}f (x)</math> = <math>\lim_{x \to \infty}\frac{4x-3}{x}</math> = <math>\lim_{x \to \infty}4 - \lim_{x \to \infty}\frac{3}{x}</math> = '''<span style="color: #EE7600 ">4</span>''' - 0 = '''<span style="color: #EE7600 ">4</span>'''<br /> |
<br /> | <br /> | ||
Das gleiche Ergebnis erhält man, wenn man den Limes von f für x gegen - <math>\infty</math> untersucht, da das Vorzeichen hier keine Rolle spielt.<br /> | Das gleiche Ergebnis erhält man, wenn man den Limes von f für x gegen - <math>\infty</math> untersucht, da das Vorzeichen hier keine Rolle spielt.<br /> | ||
| Zeile 75: | Zeile 75: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | === <big>Allgemein</big> === | + | === <big>Allgemein === |
| + | Im Applet siehst du die gebrochen rationale Funktion '''<span style="color: blue"><math>f(x)=\frac{ax+b}{x}</math></span>'''.<br /> | ||
| + | Über die Schieberegler '''a''' und '''b''' lässt sich der Graph der Funktion verändern.<br /> | ||
| + | Welchen Zusammenhang kannst du zwischen '''a''', '''b''' und der '''<span style="color: orange">waagrechten Asymptote</span>''' von <span style="color: blue">'''f'''</span> feststellen?</big> | ||
| + | |||
| + | <ggb_applet width="773" height="571" version="4.2" ggbBase64="UEsDBBQACAAIAL1e7UIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAL1e7UIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVhtb9s2EP6c/oqDPrVrbJN6d2C3aAsU65B2xdIN3b4MlETbbGRJEylbLvrjdyQlW3Fe2iRAkdgnkvf23B2PlGcv23UOG15LURZzh46JA7xIy0wUy7nTqMUodl6+eDJb8nLJk5rBoqzXTM0df+w6Bzkcjb1QC4ts7kQhi9OUsdEiTrKRTzI6StxwOnKzlHohC0iWRA5AK8VZUX5gay4rlvKLdMXX7LxMmTI6V0pVZ5PJdrsd99bHZb2cLJfJuJWZA+h5IedO93CG6q4IbT3D7hJCJ5/fn1v1I1FIxYqUO6BRNeLFk5PZVhRZuYWtyNRq7sQEYay4WK4QZugFDkw0U4VYK54qseESRQdDg1mtK8ewsUKvn9gnyPdwHMjERmS8njtkTKcu6i1rwQvVrdPOzqTXMNsIvrWq9JOx4pMpRm4jpEhyPncWLJeIRBSLGqOITtQNDqXa5TxhdT8++EBP8Q8ZxFeudSFOC13jjE6pOz2NCDkNAmJ9GRp2QJVlbrQSCKbw7Ru4xCVwqgm1xEUShnaJ2DniWeJa4lsSWB7fivuW1bc8vuXxvTtwduMD0G7iCtIepzfESRGf/oT4MQE4whkPcFIN4htQ7b0hHmi/qfFfE78bhnYYGUKJJbRbjPWXiVf4SETegxDRgVVbD7cbvVYvvcUo8n7covsonHuUNPCv23SDW1A+MrgHo4PQoi3zbz7XTHr3wnlraO9hMfQfs/cfYDAiP8PgbNJ3ulm390CuNG9Xroqvpe463tQ0HqAQ4MYMI+wTAdApkkhvUBdoAH6AQxpDqGkEnt6TPngQg+ajHpj2EsT45Zv9GkKAuvRkZDcueD4EHlDTlHzAVgSmsWGTcz3kCAIIUEhbp9qsF4If4sCLwUcHdUuLdNvwUA7HaNwFj4KnZWkEbgihC5Fui9TX3TKMte+o1IWQQKhFsS9iT7T9ECVi8DQarPCqlGIf3BXPq31WTBxFUTWqi103n66zPo6qPGLPyvTy9VGwOZOqf0YmPI0O55w9na4cgyeznCU8x8vCha4DgA3L9RY2+hdloaCvgdjOLWtWrUQqL7hSKCXhC9uwc6Z4+xa5Ze+gMW1O5xlv0lxkghV/YZFoFVoh9Ie1aUz9Ye1PO8tpWdbZxU5i5UD7D69L9CkOxy4JfUriCL+iqQM7u+L68Zj4EY0pnfqup/tPynTBu8E4DKIpCaaUBl7g6R6zu2Utsob5Zg+MtVz2kVzWIhs+v5OvyzzbZ6MqRaHesEo1tbl2oQu1RvSqWObcBNY0VbzApJdJ2V7YiHpW16ddhSNi7SfLN2Ve1lBrD/GGsexoYqnh0Y7tuYjhIYaD9CkS2X4dLyqGw9DEUsOFObeudUBpj5KS3oyQpomg8mGFmYKZO60DTSHUuR1hdYr0soNKrcCHZp1gsXVyV3XSG3XuHqJTe41XM6k+d9df/fz34PnTiiumL22B6wXTOIoC/HancWyr9Kg+Z5e8Lnhuq7DAUmjKRtptsS/tk1kj+UemVq+K7A++xA39kemeqtA1y3pwL+OpWKOgne+Cz3Rh/IlQ7WzGlzXvQ5Sbm7JNjVklwz1xbdqoeluX63fF5hNW3ZGrs0mPZybTWlS6tiHBJn/JD/WLUWJ4RGRDOQQvEUWq2xUmQpkT5Gn7DObwlLXPk2dnWAGsUasSq+z9rhZsDefoDGrDbqDLG35rcoHtFwtdt4Gcr/GyDMqUe9GseS3SfeaZuXuj602Pbtzh01mHMvmCLeuoWg4xxuVbNgSwvFqZ5NOu7NmO11cCaLT9vlhIrqCdOyPcJzsk0WD1fZl1bnVaZK5fBGAtCsMJa4aSSFkiy7xR+CqE+SwOr0LW767l4TVIlyZKBKF55UJz1DVzC9EO0oKhFV+xBo9q77BzFXbiS3zZsNtXdY3EPPwqsowXe4dZgUVoUok9tbLxADwHeHZVtML4mBY2KKAuc9/NYXKcQ/pzc3h3lrCt2TTph4fnKaJ35+kA6MY0uT8lTW1VozWtpgtz+i9K4zS2WNy/rNekXbTXhKuZtfMD2YcksT+/qBtdSyT5wc2oVez20TnKsjvoi1Jzkz5Jmn7FnB8M3ZSL4O5c8P8KKyLtCYThy0Uq1PejvehivW+X8Au08BySZzCB9qaAL5rCNFrnoOIhIQ+oibgm3YXh/iE3lyT9e8JdO+v+8RxGbDI8W8xFsft56MX/UEsHCLads/dpBgAAzhIAAFBLAQIUABQACAAIAL1e7ULWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAvV7tQrads/dpBgAAzhIAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAAABwAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" useLocalJar="true"/> | ||
| + | <br /> | ||
| + | <popup name="Antwort"> | ||
| + | Die Funktion '''<span style="color: blue"><math>f(x)=\frac{ax+b}{x}</math></span>''' nähert sich für immer größer und immer kleiner werdende x- Werte immer mehr der '''<span style="color: orange">Gerade y = a</span>''' an. | ||
| + | </popup> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <big>Im nächsten Applet ist die Funktion <span style="color: green">'''f(x) = a ∙ e<sup>b ∙ x'''</sup> + c</span> abgebildet.<br /> | ||
| + | Welcher Zusammenhang besteht hier zwischen den drei veränderlichen Zahlen '''a''', '''b''' und '''c''' und der <span style="color: orange">'''waagrechten Asymptote'''</span> von '''<span style="color: green">f</span>'''?<br /> | ||
| + | </big> | ||
| + | |||
| + | <ggb_applet width="773" height="569" version="4.2" ggbBase64="UEsDBBQACAAIAJ1j7UIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAJ1j7UIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vjdbts2FL5On+JAV90W26RI/biwW7QFhnVIu2Lphm4XBSiJttnIkiZRiV30cu+zd9qT7JCUbMX5WZsMW5fEpiidv++cw49UZk826xzOZd2osph7dEw8kEVaZqpYzr1WL0ax9+Txg9lSlkuZ1AIWZb0Weu7xse/t9XA2ZqFRVhla4YwkMlmMRBTIEU/i6SiJMj5iMU+liJjMCPcANo16VJSvxFo2lUjlabqSa3FSpkJbmyutq0eTycXFxbj3Pi7r5WS5TMabJvMAIy+audddPEJzl5QumBX3CaGTty9PnPmRKhotilR6YFC16vGDo9mFKrLyAi5UpldzLyYIYyXVcoUwQ8Y8mBihCrFWMtXqXDaoOphazHpdeVZMFOb5kbuCfAfHg0ydq0zWc4+M/cCDslay0N1T2nmZ9PqzcyUvnCFzZX1wMo0w6apRSS7n3kLkDeJQxaLGHGIIdYvTRm9zmYi6n+8joMf4iwLqgzS2EKUDPvcYY8fx9Dgi5DgIiAtl6NcDXZa5NUogmMLHj+ATn8CxGagbfBzC0D0i7h5hbvDdwN0QOBnu1LkT5U6GOxnOboHZzfc4uxuXgPYw2RAmRXzmE+LH4j/AGQ9wUgPiI1ATvR0YmLipjd8MvJuGbhrZgRI30O5hbL5svsJ7ImJ3QkQHXl073Oz0Srv0HqOIfbpH/144dyj961D6wQ0o75nc3ikNBk7Rl/2znysu2WfhvDG1n+Ex5PdZ+ndwGJF/w+Fs0hPdrFt70KyMbNeuWq4bwzpsaokHKAS4MMMIeSIAOsUhMgvUBxoAD3BKYwjNGAEza5IDgxiMHGVg6SWI8Yvb9RpCgLbMzcgtXGAcAgbUkhIHpCKwxIYk5zOUCAIIUMl4p8YtC4GHOGExcAzQUFpkaIOhHs7RuQ+MAjO6NAI/hNCHyNAi5YYtw9jEjkZ9CAmERhV5ETnR8SFqxMAMGuzwqmzULrkrmVe7qtg8qqJqdZe77n66zvo86vJAPCvTs2cHyZai0f01CuFmtN/k3OZ0aQ88muUikTmeFE5NHwCci9wsYWt/URYa+h6I3b1lLaqVSptTqTVqNfBenIsToeXmW5Ru+gCta7s1z2Sb5ipTovgZm8SYMAah36ktMfU7NZ9S5yUtyzo73TbYObD5VdYlxhRPxyEnjPux79OQotq2e0LZmE9xXyWMTGng47JuUmE6nk/H0+EP7rzb7lFAxmT4Q7nzLM93yMRGNn0ql7XKhtcvmmdlnu3KUZWq0M9FpdvaHrowuNpAelosc2kza1kVjy/pWVJuTl1KmbP1ZlvhjDj/yfJ5mZc14Hr0AzxhLLsxcaOVMYHtpIiVIVaC9DVS2e45nfpWwo6JG60UFt2F1gGlPUpKejeqsSyCxoctZjtm7m08aAulT9wM21OlZx1U6hRetesEu63Tu2yTXmtzexebJmo8mDX6bXf4Nde/DK7frKQW5sgW+CyYxlEU4Lc/jWPXpgcNOjuTdSFz14YFtkJbto1bF7vePpq1jXwt9Oppkf0ol7iiXwtDqhpDc6L78DKZqjUquvtd8oVpjJ8QqrubyWUt+xTl9pzsSmOfkuGiuHLbmvq2LtcvivM32HUHoc4mPZ5Zk9aqMr0NCbL8mdz3L2ZJ4B6RDfUQfIMoUsNXWAhtt5CHm69gDkK+SzbwDaQeiFavSmyzl9taiTWcYDRoDvnA9Dd83+YKCRg73RBBLtd4WgZt+71o17JW6a70wh69Mfa2g2fKZwGaskOZvEfSOmiXfZLx8Q0rAkRerWz1O27JxVbWlzJorb0ss95x5zY3J31YK2TrES7VtdggbaC9pCnzVuO7Dpas2L/ruMg6WsOjjuk+o8HtO9XWrDx7tVAbueMSzJ36gF12uWX2S1Mj157h20Rj+UN3TGEvvlNZJotduKLALrO1QtasHF5Appduse1UK8RvOWrQIV1l/rZGyWGNRvga9OUUKfgHiuTz/3uR0sMikS9xIfHPrlE4/dQaDWj6PyzSpqrRmzHTJXmBp7NNtSdR+Br+/P2Pdw8TvMA7lk4nV8q7aAtLwd7ezN1rSQN2pZrk1mr+sFg0Upv8c5f8kR/cVmxblMMt8NoqBLdV4fZMZl0mt5jGtDdjnFyXQHd/p3mX5PUnMepHd04fi236eHxt9vzBFt8YcdJvGmb8YJmW3DWZeKr9rXAqjTtMYfZylSp9mOrJcNO3R/juv3aP/wJQSwcI3oqARXcGAABlFAAAUEsBAhQAFAAIAAgAnWPtQtY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACACdY+1C3oqARXcGAABlFAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAA4HAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" useLocalJar="true"/> | ||
| + | <br /> | ||
| + | <popup name="Antwort"> | ||
| + | Die Funktion '''<span style="color: green">f(x) = a ∙ e<sup>b ∙ x</sup> + c</span>''' nähert sich für immer '''kleiner''' werdende x- Werte immer weiter der '''<span style="color: orange">Gerade y = c</span>''' an, sofern '''b > 0''' ist. | ||
| + | Für '''b < 0''' nähert sich '''<span style="color: green">f</span>''' für immer '''größer''' werdende x- Werte immer mehr der '''<span style="color: orange">Gerade y = c</span>''' an. | ||
| + | </popup> | ||
| + | <br /> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Allgemein gilt:<br /> | Allgemein gilt:<br /> | ||
| − | Nähert sich der Graph einer Funktion für '''immer größer werdende''' x-Werte einer '''Zahl''' | + | Nähert sich der Graph einer Funktion für '''immer größer werdende''' x-Werte einer '''Zahl''' <span style="color: orange">G</span> immer weiter an, so nennt man <span style="color: orange">G</span> den '''Grenzwert von f''' für x gegen + <math>\infty</math>:<br /> |
| − | In mathematischer Schreibweise: <math>\lim_{x \to \infty}f (x)</math> = | + | In mathematischer Schreibweise: <math>\lim_{x \to \infty}f (x)</math> = <span style="color: orange">G</span><br /> |
<br /> | <br /> | ||
| − | Die Gerade '''y = | + | Die Gerade '''<span style="color: orange">y = G</span>''' ist dann eine '''<span style="color: orange">waagrechte Asymptote</span>''' für den Graphen von f.<br /> |
| − | + | Auf gleiche Weise definiert man den Grenzwert einer Funktion für '''immer kleiner werdende''' x- Werte, also für x gegen - <math>\infty</math>, mit <math>\lim_{x\rightarrow\ -\infty} f(x)</math>. | |
</div> | </div> | ||
Version vom 13. Juli 2013, 12:36 Uhr
|
Will man anhand des Funktionsterms Aussagen über den Verlauf des Graphens machen, muss man auch wissen, wie sich die Funktion für immer größer und immer kleiner werdende x- Werte verhält. Bei ganzrationalen Funktionen hast du bereits vier Fälle über den charakteristischen Verlauf einer Funktion kennen gelernt.
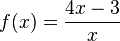
Diese Vermutung lässt sich mathematisch untersuchen:
 : :
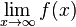
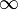 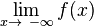 wird untersucht, wie sich f (x) für immer kleiner werdende x- Werte verhält.
|
AllgemeinIm Applet siehst du die gebrochen rationale Funktion
Allgemein gilt: Auf gleiche Weise definiert man den Grenzwert einer Funktion für immer kleiner werdende x- Werte, also für x gegen - |
Übung
Manipulationen an Funktionen |
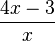 scheint sich für immer größer werdende x- Werte der Gerade
scheint sich für immer größer werdende x- Werte der Gerade 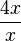 -
-  =
= 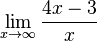 =
= 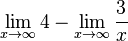 =
=