Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Mathematik Klasse 8
In diesem Lernpfad erfährst du mehr über lineare Funktionen. Du wirst die allgemeine Funktionsgleichung linearer Funktionen untersuchen und lernen, wie der Graph der Funktion von den Parametern der Funktionsvorschrift abhängt. Die zentralen Begriffe hierzu sind die Begriffe Steigung und Achsenabschnitt. Weiterhin wirst du lernen, wie man die Funktionsgleichung einer linearen Funktion bestimmen kann, wenn man den Graphen hat, und wie man den Graphen zu einer gegebenen Funktionsvorschrift zeichnet. Hierbei wird das sogenannte Steigungsdreieck wichtig sein.
Inhaltsverzeichnis |
Die Funktionsvorschrift
Vorlage:UntersuchenVorlage:Protokollieren
Die allgemeine Form einer Funktionsgleichung einer linearen Funktion ist f(x)= m x + b.
Im folgenden sollst du untersuchen, welche Bedeutung m und b haben.
|
Die allgemeine Form einer Funktionsgleichung einer linearen Funktion ist f(x)= m x + b. Dabei heißt m Steigung und b ist der y-Achsenabschnitt der linearen Funktion. |
Die Steigung einer linearen Funktion
Vorlage:UntersuchenVorlage:Protokollieren
Die Steigung m einer linearen Funktion f: y = m x + b gibt an, um wie viel sich der y-Wert ändert, wenn sich der x-Wert um 1 ändert. Wenn sich der x-Wert um 2 ändert, ändert sich natürlich der y-Wert entsprechend um 2m. In dem Bild ändert sich der y-Wert um 3, wenn sich der x-Wert um 2 ändert. Die Steigung der Geraden ist daher 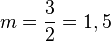 , siehe dazu auch folgende Graphik. Die Dreiecke, die sich beim Einzeichnen ergeben, nennt man Steigungsdreiecke.
, siehe dazu auch folgende Graphik. Die Dreiecke, die sich beim Einzeichnen ergeben, nennt man Steigungsdreiecke.
Graphen zeichnen
Um den Graphen einer linearen Funktion f: y = m x + b zu zeichnen, markierst du den Achsenabschnitt als Punkt. Dann zeichnest du von dort ausgehend ein Steigungsdreieck ein und markierst einen zweiten Punkt. Wenn die beiden Punkte verbindest, erhältst du den Graphen der linearen Funktion. Dabei kannst du das Steigungsdreieck zeichnen, indem du vom Achsensabschnitt eine Einheit nach rechts gehst und dann um m Einheiten nach oben (bzw. unten, wenn m negativ ist) gehst. Es kann aber auch sinnvoll sein (z. B. wenn m ein Bruch ist), größere Steigungsdreiecke zu zeichnen und mehr als eine Einheit nach rechts zu gehen und dann entsprechend mehr Wenn z. B. die Steigung m=1/3 ist, kann man um 1 nach rechts und um 1/3 nach oben gehen, oder aber um 3 nach rechts und 1 nach oben (das ist das gleiche wie drei Steigungsdreiecke hintereinander) - man erhält die gleiche Gerade (siehe Zeichnung). Meist wird die Zeichnung genauer, wenn man ganzzahlige Werte nach oben bzw. unten abtragen kann.
Vorlage:Protokollieren
Seite 118/1, Welche Spezialfälle treten bei dieser Aufgabe auf?
Seite 118/6
Funktionsgleichungen bestimmen
Vorlage:ProtokollierenVorlage:Begründen In diesem Abschnitt sollst du lernen, wie man anhand des Graphen die Funktionsvorschrift einer linearen Funktion bestimmen kann.
In einem ersten Schritt sollst du zu den Graphen von linearen Funktionen die entsprechende Funktionsvorschrift zuordnen.
Vorlage:Aufgaben-M
Jetzt sollst du selbst die Geradengleichungen aufstellen:
Vorlage:Aufgaben-M
Vorlage:Protokollieren
Felix ist ein Schüler aus der Parallelklasse. Er ist neugierig, was wir so im Mathe-Unterricht machen.
Schreibe ihm einen Brief, in dem du ihm erklärst, was lineare Funktionen sind und wie man mit dem Graphen einer linearen Funktion die zugehörige Funktionsgleichung aufstellt.
Vorlage:Protokollieren
Seite 118/3

