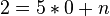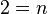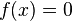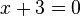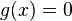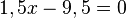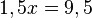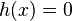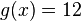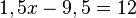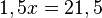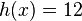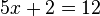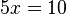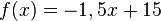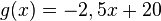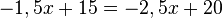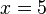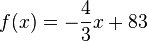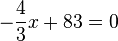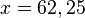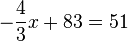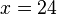Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Lineare Funktionen
|
In diesem Lernpfad kannst du dein Wissen über lineare Funktionen vertiefen und dieses anwenden. In Aufgabe 1-5 wiederholst du dabei noch einmal, wie lineare Funktionsgleichungen aufgestellt werden und wie man einen Graphen skizziert. Außerdem kannst du dich in Aufgabe 3 noch einmal mit Wertetabellen zu linearen Zuordnungen beschäftigen. Die Aufgaben 6 und 7 bieten dir die Möglichkeit, das Gelernte im Sachkontext anzuwenden. |
Inhaltsverzeichnis |
Lineare Funktionen im Überblick
|
Fülle folgenden Lückentext aus, indem du auf die leeren Felder klickst und die richtige Antwort auswählst |
Vom Graphen zur Funktionsgleichung
|
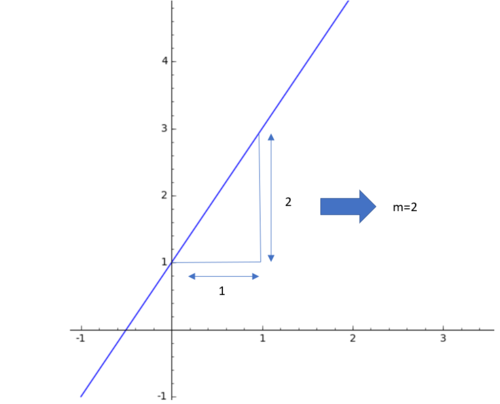
Ordne den folgenden Graphen die entsprechenden Funktionsgleichungen zu, indem du die zusammengehörigen Felder aufeinander legst. |
Wertetabellen und lineare Funktionen
|
Bestimme anhand der Tabellen die zugehörigen Funktionsgleichungen und tippe sie in die grauen Felder ein. |
Schnittpunkt zweier Geraden
|
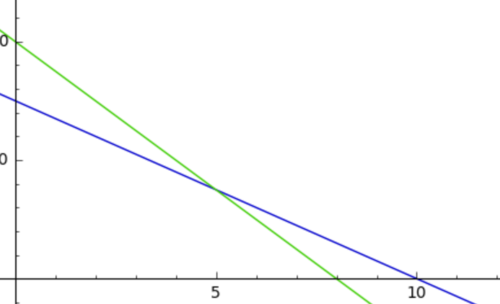
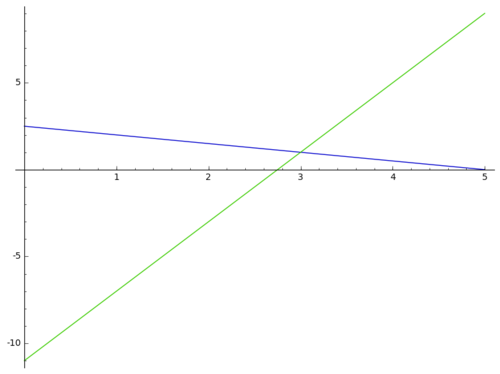
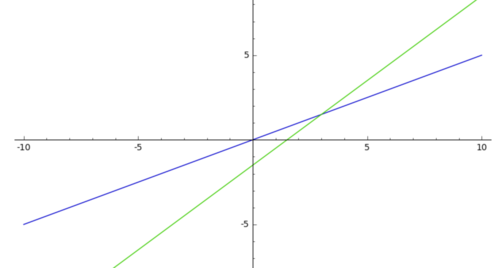
Bestimme die Schnittpunkte von zwei Geraden zuerst zeichnerisch und dann rechnerisch in deinem Heft. a) b) |
Funktionsgleichung aufstellen anhand zweier vorgegebener Punkte
|
Betrachte die drei Geraden f,g und h, die jeweils durch die angegebenen Punkte verlaufen. 1) Gerade f verläuft durch 2) Gerade g durch 3) Gerade h durch Notiere die Rechnungen und Antworten der folgenden Aufgaben in deinem Heft: |
Textaufgaben
|
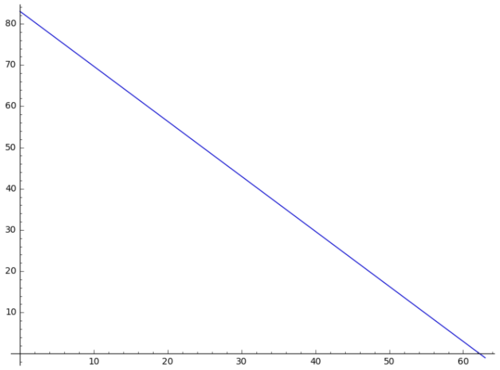
Eine 15cm lange Kerze A braucht 10 Stunden, um vollständig abzubrennen. Eine weitere und dünnere Kerze B ist 20cm lang und brennt in nur 8 Stunden vollständig ab. a) Stelle für jede Kerze eine Funktionsgleichung auf, mit der man die Kerzenhöhe nach x Stunden berechnen kann und zeichne einen Graphen. b)Welche Höhe haben die Kerzen nach 3 Stunden? c) Die Kerzen werden gleichzeitig angezündet. Nach wie vielen Stunden sind die Kerzen gleich hoch? d) Vergleiche die drei Methoden, aus dem Aufgabenteil c) und überlege dir, welche Vor- und Nachteile diese Methoden haben.
|
|
Aus einer zylinderförmigen Regentonne wird das Wasser gleichmäßig abgelassen. Nach 6 Minuten beträgt die Wasserhöhe noch 75cm, nach weiteren 15 Minuten sind es noch 55cm a) Warum handelt es sich hierbei um eine lineare Funktion? c) Bestimme den Zeitpunkt, in dem das Wasser vollständig abgelaufen ist. d) Zu welchem Zeitpunkt beträgt die Wasserhöhe 51cm? e) Schau dir die Aufgabenteile c) und d) nochmal genauer an. Kannst du dein Vorgehen begründen?
|
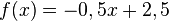 und
und 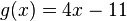
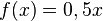 und
und 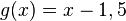
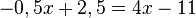 Rechne beidseits +11 und +0,5x.
Rechne beidseits +11 und +0,5x. 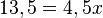 Teilen durch 4,5 liefert
Teilen durch 4,5 liefert 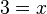
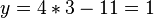
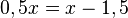 Rechne beidseits -x.
Rechne beidseits -x. 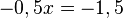 Teilen durch -0,5 liefert
Teilen durch -0,5 liefert 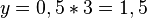
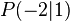 und
und 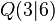 .
.
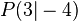 und
und 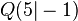 .
.
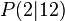 und
und 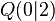 .
.
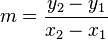
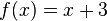
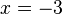
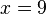
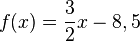
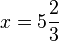
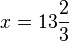
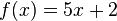
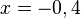
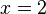
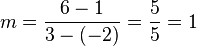
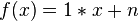 ein und erhalten:
ein und erhalten: 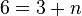 und somit ist
und somit ist 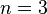 .
. 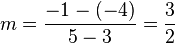
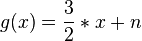 führt zu
führt zu 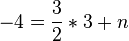
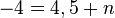
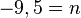
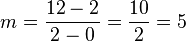
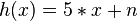 führt zu
führt zu