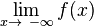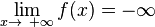Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Benutzer:RMG Gruppe 2: Unterschied zwischen den Versionen
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<center>Bist du bereit für das <colorize> ''ULTIMATIVE MATHE-ABENTEUER''?</colorize></center><br /> | <center>Bist du bereit für das <colorize> ''ULTIMATIVE MATHE-ABENTEUER''?</colorize></center><br /> | ||
| − | <center>Dann bist du hier genau richtig du kleiner Mathe-Freak!</center><br /> | + | <center>Dann bist du hier genau richtig, du kleiner Mathe-Freak!</center><br /> |
<center>Mach dich bereit für spannende Ausflüge in die faszinierende Welt der Mathematik!</center><br /> | <center>Mach dich bereit für spannende Ausflüge in die faszinierende Welt der Mathematik!</center><br /> | ||
<center>Auf in den '''ZAHLENKAMPF'''! :)</center><br /> | <center>Auf in den '''ZAHLENKAMPF'''! :)</center><br /> | ||
| Zeile 15: | Zeile 15: | ||
<center><div class="lueckentext-quiz">Definition: | <center><div class="lueckentext-quiz">Definition: | ||
Nähert sich der Graph einer Funktion f für '''immer größer werdende''' x-Werte einer '''Zahl''' G immer weiter an, so nennt man G den '''Grenzwert''' für x gegen +∞:<br /> | Nähert sich der Graph einer Funktion f für '''immer größer werdende''' x-Werte einer '''Zahl''' G immer weiter an, so nennt man G den '''Grenzwert''' für x gegen +∞:<br /> | ||
| − | In mathematischer Schreibweise:<math>\lim_{x\rightarrow\infty} f(x) = G </math> Auf gleiche Weise definiert man den Grenzwert einer Funktion f für '''immer kleiner werdende''' x-Werte, also für x gegen -∞, mit <math> \lim_{x\rightarrow\ -\infty} f(x) | + | In mathematischer Schreibweise:<math>\lim_{x\rightarrow\infty} f(x) = G </math><br /> Auf gleiche Weise definiert man den Grenzwert einer Funktion f für '''immer kleiner werdende''' x-Werte, also für x gegen -∞, mit <math> \lim_{x\rightarrow\ -\infty} f(x) |
</math> | </math> | ||
| − | Nähert sich eine Funktion f für immer größere x-Werte '''keiner festen Grenze''' an, sondern fällt beispielsweise gegen '''-∞''',so heißt f divergent.</div></center> | + | Nähert sich eine Funktion f für immer größere x-Werte '''keiner festen Grenze''' an, sondern fällt beispielsweise gegen '''-∞''',so heißt f divergent. <math>\lim_{x\rightarrow\ +\infty} f(x) = -\infty </math> </div></center> |
Aktuelle Version vom 19. Juli 2013, 09:44 Uhr
Definition:
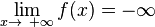
Nähert sich der Graph einer Funktion f für immer größer werdende x-Werte einer Zahl G immer weiter an, so nennt man G den Grenzwert für x gegen +∞:
In mathematischer Schreibweise: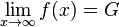
Auf gleiche Weise definiert man den Grenzwert einer Funktion f für immer kleiner werdende x-Werte, also für x gegen -∞, mit