Dieses Wiki, das alte(!) Projektwiki (projektwiki.zum.de)
wird demnächst gelöscht.
Bitte sichere Deine Inhalte zeitnah,
wenn Du sie weiter verwenden möchtest.
Gerne kannst Du natürlich weiterarbeiten
im neuen Projektwiki (projekte.zum.de).Übungen: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| + | __NOTOC__ | ||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="900px" valign="top"> | ||
<colorize>Gruppe 1</colorize> | <colorize>Gruppe 1</colorize> | ||
| Zeile 31: | Zeile 37: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="900px" valign="top"> | ||
<colorize>Gruppe 2</colorize> | <colorize>Gruppe 2</colorize> | ||
| Zeile 57: | Zeile 69: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
<colorize>Gruppe 3</colorize> | <colorize>Gruppe 3</colorize> | ||
| Zeile 84: | Zeile 102: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
<colorize>Gruppe 4</colorize> | <colorize>Gruppe 4</colorize> | ||
| Zeile 113: | Zeile 137: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="700px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
<colorize>Gruppe 5</colorize> | <colorize>Gruppe 5</colorize> | ||
| Zeile 137: | Zeile 167: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
<colorize>Gruppe 6</colorize> | <colorize>Gruppe 6</colorize> | ||
| Zeile 189: | Zeile 225: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
<colorize>Gruppe 7</colorize> | <colorize>Gruppe 7</colorize> | ||
| Zeile 233: | Zeile 275: | ||
<br /> | <br /> | ||
| − | < | + | </td></tr></table></center> |
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background:#836FFF;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="900px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
<colorize>Gruppe 8</colorize> | <colorize>Gruppe 8</colorize> | ||
| Zeile 272: | Zeile 320: | ||
<br /> | <br /> | ||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
<br /> | <br /> | ||
{| | {| | ||
Version vom 23. Juli 2013, 16:42 Uhr
|
Gruppe 1
|
|
Gruppe 2
Definition:
Nähert sich der Graph einer Funktion f für immer größer werdende x-Werte einer Zahl G immer weiter an, so nennt man G den Grenzwert für x gegen +∞:
|
|
Gruppe 3 Zuordnugsquiz zur Symmetrie von Funktionen
Symmetrie: Bei der Achsensymmetrie gilt: f(x)= f(-x). Bei der Achsensymmetrie dürfen im Funktionsterm nur x- Potenzen mit geraden Exponenten auftreten.
Bei der Punktsymmetrie gilt: f(-x)= -f(x). Bei der Punktsymmetrie dürfen im Funktionstern nur x- Potenzen mit ungeraden Exponenten auftreten.
|
|
Gruppe 4 Wie verläuft die Funktion f(x)= 2x3+x4+7? (!von links unten nach rechts oben) (!von links unten nach rechts unten) (von links oben nach rechts oben) (!von links oben nach rechts unten) Wer ist die tollste Mathelehrerin überhaupt? (unsere) (unsere) (unsere) (unsere) Welche Symmetrie besitzt die Funktion f(x)= x3? (!Achsensymmetrie zur y-Achse) (Punktsymmetrie zum Ursprung) (!Keine Symmetrie) Was ist die Voraussetzung für eine achsensymmetrische Funktion? (!Verlauf durch den Ursprung) (Alle Exponenten gerade) (!Alle Exponenten ungerade) (Größter Exponent ist gerade) Wie beeinflusst der Faktor t=2 die Parabel der Funktion f(x)= tx2+5? (!Sie wird +2 nach oben verschoben) (Sie wird enger) (!Sie wird weiter) (!Sie wird -2 nach unten verschoben) Wie heißt der Term der Funktion f(x)=x8-3 , wenn sie an der x-Achse gespiegelt wird? (-x8-3) (!x8+3) (!-x8+3) (!x-8-3)
|
|
Gruppe 5 Memory zu Verschiebungen
|
|
Gruppe 7 Kreuzworträtsel zu Manipulationen an Funktionen
|
|
Gruppe 8 Lückentext-Quiz zum Thema "Manipulationen an Funktionen"
Alle Exponenten, die in einem Funktionsterm auftauchen müssen gerade sein, um Achsensymmetrie zur y-Achse vorweisen zu können. Wenn der Funktionsterm einer geraden Funktion (= nur gerade Exponenten) vorliegt, kann man auf den Graphen der Funktion schließen, da alle gleich weit vom Ursprung entfernte x-Werte zugleich Achsensymmetrie zur y-Achse bedeuten. Daraus folgt: f(x)= f(-x).
Bei einer Verschiebung eines Graphen der Funktion f wird der Graph um a Einheiten in x-Richtung bzw. um b Einheiten in y-Richtung verschoben. Ist a>0 wird der Graph nach rechts verschoben, bei a<0 nach links. Für b>0 wird der Graph nach oben, in positive Richtung, bei b<0 nach unten in negative Richtung verschoben.
Bei einer Funktion der Form g(x)= -a⋅f(x) handelt es sich bei a um den Streckungsfaktor, der den Graphen in y-Richtung streckt. Zudem wird der Graph durch das negative Vorzeichen an der x-Achse gespiegelt.
Kommt der Graph einer Funktion f(x) einer Zahl G immer näher, so ist G der Grenzwert der Funktion f für x Fehler beim Parsen(Lexikalischer Fehler): \rightarrow\
+
|
| Zurück zur Übersicht |
Manipulationen an Funktionen
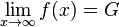
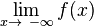 Nähert sich eine Funktion f für immer größere x-Werte keiner festen Grenze an, sondern fällt beispielsweise gegen -∞,so heißt f divergent.
Nähert sich eine Funktion f für immer größere x-Werte keiner festen Grenze an, sondern fällt beispielsweise gegen -∞,so heißt f divergent. 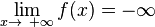
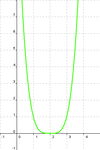
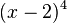
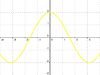
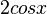
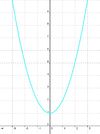
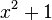
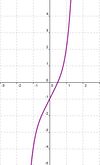
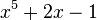
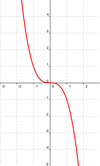
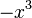
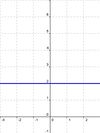
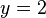
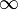 .
. 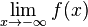 , gesprochen: "Limes von f(x) für x gegen -
, gesprochen: "Limes von f(x) für x gegen -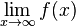 = -
= -
