|
|
| (35 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | __NOTOC__ | | __NOTOC__ |
| − | === Wiederholung: Verschiebung von Parabeln === | + | <div style="padding:1px;background:#1C86EE;border:0px groove;"> |
| − | Du weißt bereits, wie sich Parameter auf die Graphen von Parabeln auswirken können.
| + | |
| | | | |
| − | Im folgenden Applet kannst du über die Funktionen h bzw. g die Verschiebung nach links/rechts (durch den Schieberegler a) bzw. nach oben/unten (durch den Schieberegler b) beobachten.<br>
| |
| − | Klicke auf die jeweiligen Checkboxen im Applet, um die Funktionen anzuzeigen oder auszublenden.
| |
| − |
| |
| − | In der Funktion j werden beide Arten der Verschiebung zusammengeführt.
| |
| − |
| |
| − | <ggb_applet width="1029" height="619" version="4.2" ggbBase64="UEsDBBQACAAIAFintkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFintkIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVltbxs3Ev6c/orBfigSnCXxbd9yUoq2QHEFnDao06LohyuoXUqivdrV7VKyHORX9Sf0l92Q3JVWdqyTawXXODbF5XCG88zMw1l7/NV2WcBG1Y2uyklAhyQAVWZVrsv5JFib2SAJvnrzxXiuqrma1hJmVb2UZhKIIQv2+3A25JHdrPNJkCk2UyIhA5nLeCBmeTZIUh4NYjFLWBopFk6zAGDb6Ndl9YNcqmYlM3WVLdRSXlaZNE7nwpjV69Ho9vZ22FkfVvV8NJ9Ph9smDwBPXjaToP3wGtUdbLrlTpwRQke/vr306ge6bIwsMxWA9Wqt33zxYnyry7y6hVudmwViQEQYwELp+QL9jFkSwMhKrdDZlcqM3qgG9/amzmmzXAVOTJZ2/YX/BMXOnwByvdG5qicBGTLBKAlZxGkYJ6mIRQBVrVVpWmHaGh116sYbrW69XvvJmRQkjTEIutHTQk2CmSwa9EuXsxoxxRPVa5w25q5QU1l38/2B6AV+oYD+oKwuDJ4HYhJEQlzQiF/EhFyEIfFn6RsOwFRV4bQSCFP4+BEYYQQu7ED9wHCIIr9E/DPC/cD8IPwQehnhtwsvKryM8DKCH/Gzne8dbR8ceNr5yfp+kgtygY5fOOfv+Zj0fKTWgY9A7cndwMGembqz20G008hPYzdQ4gfaLib2h8Mqeoo3D8PGO2d43xlUfmG/o0ccoj2jXucTbHYWKWHpafixZ0WMPxov9ph7TwL1YYrsPAx7BkPMf/vffT8wyZ/k4+OYnm4xEs+p979gMCYHpd7VuR9pOx6D4WyHGo86Bhy3B4JmYWXbXDZq2dgj8tQRElAIsWijGPkjBJriENviZUBDECFOaQKRHWPgtl4FcEjAylEOjnbCBH8IV8sRhKjLPox9UQMXEHKgjqwEIArgCA8xYRwlwhBC3GStU2uWRyAinPAEBB7QUl1sKYXjPpyjcQacArd7aQwsgohBbOmSCsuiUWLPjkoZRAQiuxX5ErnS8yTuSIBbb7AKVlWjd+AuVLHaRcXhqMvV2rTYtc+zZd7haKp74nmV3XyzA7tdUbIxfTG8p/bXob+3Dm7LF+NCTlWBTcWVzQSAjSxskTsLs6o00GWB8M/mtVwtdNZcKWNwVwPXciMvpVHb71C66Ww70+4WH6t1Vuhcy/IXTBOrwiqE/aVueau71MOUejNZVdX51V2DyQPb31Rd4d0msI9haZKyMKJpwkNE9M4vcZIO45SRtP3CK6LJpM36iAxF2vuH1/Ldfin0xtRm543cqqZDfF7bQmuxtJPvm2+qYv9oVenSfCtXZl27pgypsbZufF3OC+XgdGSL7U12M622Vx5H7nW9v1vhjPgDTOffVkVVA5YhC7HHmbfj1I9Oxp5sJ0WcDHESpAuMznfrNGVOwo1TPzopjLQ/Wusp7dykpDOjG0cwqLxfxi5NbK+0LrW57CZGZzetp9TL/7BeTjHD2m2HKumZVI5H93JqfKPqUhU+cUqM5LpaNz6Vd+n4Yrxu1DtpFl+X+U9qjmX4TlomNKjai+5PnKtML3Gjf95CJ21Yf8aj+qe5mteq87BwXbAH1q2Sfho/eOxUfVdXy+/LzXvMmXtHHY86f8ZNVuuVTU2YIjXfqH325bqRSOx5fx8636AXmSUZBNJYEH9B/7KFVtM1Ktngc+s2Yl0GINdmUWG2vL2rtVzCJR4L9WIto88M3kqN7In5amt4u6pVY18pfNQArSLZbC0lvdy+ggls//2SvXKHUIVaYr8MxmX4bF264+zCPXPNuI0rVNNrJKJ76bCPAi4/kvAgi9VC2na9BbSQd6o+gNhp+3E2a5SBrdtzZxNqv/a2ytUh2+mtyu9nwr5eDLLeDbb8mIdYmaYtX/fhXzrPVdmqx+T0ADyAolwvVa2znafSIYEG1112dO48FZ2ONDw+Ie0BRI8CtAehlWsK+yIES43uDLCnWcqte6uQ06Yq1gbfBTHpy/27oD/cjsutBxbuJEmHLeRxaD85cDtxTDr9Aev0BKjZMahtIWGdumzHm2Ll/QW83pRnm93WFfrvOLpXY6eGaXq2MPkktuGxxE7EyWHa53FyJI/PHMKUtiFkKTkawh7F/h9jeI+hJsF7tTW0Jakv/7OuzD87qvrzDz//BF1hH2OCQw3HI91z/vl8tY8lOcJJnw4k2KClJHQhE+x4jk+xUVdyT8rZ7/R+lvccO2Oen8rXSUKdI0l4DJ6utTrITb+CbZkFxUnPd3GHf8D0acjkZ8TlCE2fjouvyVCcAZeFx+XlFgYgX/35x9OQUedExibJDpm/mjLMkyONzoDN9T1sPpk5Dzhn0fLNIbKuNYITeqPFyb0Rdnq59qSJ0j+2wvlnybkBjf09cLR9eman9ADKeQvlvNdfuiCcAuT8mUBaPvwctDZg7H83oudG8rpF8vpBUp6M5/Uz8fxMJS98Xn76Cv1MaNqmgB20FXendxPs79dNNEbW5p39VYbrIAZkyKkIBY/iJKZExG3GimHCOCFpHMUkZQKL4IP/q9RJgPEDwLanA8b/9oClQ05CllLCGeH2n4PLwohIxSyJ45CHUZIy/hhko/5ru/u9WftXtTf/BVBLBwi9RnxEkwcAAAUcAABQSwECFAAUAAgACABYp7ZC1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAFintkK9RnxEkwcAAAUcAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAKggAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| |
| − | <br>
| |
| − | <br>
| |
| − |
| |
| − |
| |
| − | <popup name="Extra-Aufgabe">
| |
| − | <div class="multiplechoice-quiz">
| |
| − |
| |
| − | Wie wirken sich die beiden Parameter a und b auf den Scheitelpunkt S(x<sub>0</sub>/y<sub>0</sub>) von j: x -> (x - a)² + b aus?
| |
| − | (!S(-a/-b)) (S(a/b)2) (!S(-a/b)) (!S(a/-b))
| |
| − |
| |
| − | </div>
| |
| − | </popup>
| |
| − |
| |
| − |
| |
| − | Auch andere Funktionsgraphen lassen sich derartig verschieben. <br>
| |
| − | Im folgenden wollen wir untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.
| |
| − | <br>
| |
| − | Fülle parallel zum Lernpfad das Arbeitsblatt aus, auf dem alle wichtigen Informationen zusammengefasst werden:
| |
| − | <br>
| |
| − | [[Datei:AB Verschieben.pdf]]
| |
| − | <br>
| |
| − |
| |
| − | === Verschiebung nach links/rechts ===
| |
| − |
| |
| − |
| |
| − | Fülle den ersten Abschnitt auf deinem Arbeitsblatt aus:<br />
| |
| − | <br>
| |
| | | | |
| | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| | + | <tr><td width="800px" valign="top"> |
| | {| | | {| |
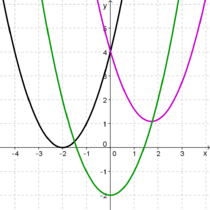
| − | | + | | valign="top"|In der 9. Klasse lernst du, welchen Einfluss die Parameter '''<span style="color: #FF7F00 ">a</span>''', '''<span style="color:#FF7F00 ">b</span>''' oder '''<span style="color:#FF7F00 ">c</span>''' auf eine Parabel, also auf den Graphen einer quadratischen Funktion mit dem Funktionsterm<br /> |
| − | |width="40%"|[[Datei:Verschiebung nach rechts.png|400px]] | + | f (x) = '''<span style="color:#FF7F00 ">a</span>'''x<sup>2</sup> + '''<span style="color: #FF7F00 ">b</span>'''x + '''<span style="color: #FF7F00 ">c</span>''',<br /> |
| − | | + | haben.<br /> |
| − | |width="3%"|
| + | |
| − | | + | |
| − | |valign="top"|Vergleiche die beiden Graphen an den vorgegebenen Werten:<br>
| + | |
| − | | + | |
| − | *h('''1,5''') = -3,375 = f (-1,5) = f ('''1,5''' - ____)
| + | |
| | <br /> | | <br /> |
| − | *h(3) = _____ = f (___) = f (_____ - _____)
| + | Oft wird auch die Scheitelform einer quadratischen Funktion<br /> |
| | + | f (x) = (x - '''<span style="color:#FF7F00 ">d</span>''')<sup>2</sup> + '''<span style="color: #FF7F00 ">e</span>'''<br /> |
| | + | betrachtet.<br /> |
| | + | In diesem Fall sind die Parameter '''<span style="color: #FF7F00 ">d</span>''' und '''<span style="color:#FF7F00 ">e</span>''' ausschlaggebend für die Lage der zugehörigen Parabel. <br /> |
| | <br /> | | <br /> |
| − | *h(4) = ____________________________________________
| + | Dieses Wissen kannst du [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Wiederholung: Verschiebung von Parabeln| hier]] noch einmal auffrischen. |
| − | | + | |
| − | | + | |
| − | Wie lässt sich h(x) aus f (x) herleiten?<br>
| + | |
| − | | + | |
| − | -> h(x) = _________________________________________<br>
| + | |
| − | <br />
| + | |
| − | Für jeden x - Wert ist der Funktionswert von h gleich dem Funktionswert von f an der Stelle __________.
| + | |
| − | | + | |
| − | |}
| + | |
| − | | + | |
| − | <br>
| + | |
| − | Vergleiche deine Antworten mit der Lösung und bessere gegebenenfalls aus:<br />
| + | |
| − | | + | |
| − | {|
| + | |
| − | | + | |
| − | |width="40%"|<popup name="Graph">
| + | |
| − | [[Datei:Verschiebung nach rechts Lösung.png|400px]]
| + | |
| − | </popup>
| + | |
| | | | |
| | |width="3%"| | | |width="3%"| |
| | | | |
| − | |valign="top"|<popup name="Lösung"> | + | | [[Datei:Verschiebungen von Parabeln.png|210px|verweis=Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Wiederholung:_Verschiebung_von_Parabeln]] |
| − | Vergleiche die beiden Graphen an den vorgegebenen Werten:<br>
| + | |
| − | | + | |
| − | *h(1,5) = -3,375 = f (-1,5) = f (1,5 - 3)
| + | |
| − | <br />
| + | |
| − | *h(3) = 0 = f (0) = f (3 - 3)
| + | |
| − | <br />
| + | |
| − | *h(4) = 1 = f (1) = f (4 - 3)
| + | |
| − | | + | |
| − | | + | |
| − | Wie lässt sich h(x) aus f (x) herleiten?<br>
| + | |
| − | | + | |
| − | -> '''h(x) = f (x - 3)''' <br>
| + | |
| − | <br />
| + | |
| − | Für jeden x - Wert ist der Funktionswert von h gleich dem Funktionswert von f an der Stelle x - 3.
| + | |
| − | </popup>
| + | |
| | | | |
| | |} | | |} |
| − | <br /> | + | </td></tr></table></center> |
| − | | + | |
| − | ==== Allgemein ====
| + | |
| − | | + | |
| − | Im folgenden Applet ist die ganzrationale Funktion f: x -> x³ in schwarzer Farbe abgebildet.<br>
| + | |
| − | Verschiebe den roten Graphen der Funktion h: x -> (x - a)³, indem du über den Schieberegler den Parameter a veränderst.
| + | |
| − | | + | |
| − | Welche Auswirkungen hat eine Veränderung von a auf den Graphen von h?<br>
| + | |
| − | Was passiert, wenn a kleiner bzw. größer wird?<br>
| + | |
| − | In welche Richtung wird der Graph von h verschoben, wenn a negativ bzw. positiv ist?<br />
| + | |
| − | | + | |
| − | Vergleiche dazu die '''Wertetabelle'''!
| + | |
| − | <ggb_applet width="629" height="605" version="4.2" ggbBase64="UEsDBBQACAAIAH2ltkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAB9pbZCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b2W7bSBZ9Tn9FgQ+DBJBl1sJFGTkN7zJg9wRxJhjMwwAlsiRVmyLVJGXL6e6v6j+YL5tbVdxk2grlpMcdIbGrSN5azrkrFw9/XM0jdCvSTCbxgYX7toVEHCShjKcH1jKf7PnWj+9+GE5FMhXjlKNJks55fmCxPrHqcXDUp64aLMMDiztswL1gshcGvr/HBtTf4y5he57rDOxx6A4CCpJolcm3cfITn4tswQNxHczEnF8mAc/1nLM8X7zd37+7u+uXq/eTdLo/nY77qyy0EOw8zg6sovMWplsbdEe1OLFtvP+vq0sz/Z6Ms5zHgbCQQrWU7354NbyTcZjcoTsZ5rMDy2WOhWZCTmcA08PMQvtKaAFYFyLI5a3IYGjjUGPO5wtLi/FYXX9leiiq4FgolLcyFOmBZffdASWeR7E9IIy6A89CSSpFnBeydrHmfjnb8FaKOzOt6ukVma3G3cpMjiNxYE14lAEqGU9SYBQ2lC7hMMvvIzHmaXlc7wf34B8IyM9CzQVLGhqAgAHpUb/n2XbPcYqtNNYlGxYtjutVixP1snbPLhclzUXhfA9O9PROHqzoWyhPkkhPiEGd6DcEDTENReg33XHMMSsOXXPo6QbbpsHFRV/9GqgDdxs0bQ5pCYY2wcDkPfXjPgEINxY1c27DYKW0gbPOH3tiOdbgz0aOxk1sYqOearBpCDSuay7Z5hxwqxtiGmYax8gwM5wZUWZkmJFh9GsAkhIgtlkNkPhOD3vOkyDxVppsLVq5AnYainTABdR//dNakm7lCi3jecaKLvsaj3/Ggp69Zjul4ZgWF+0mGr7Zpob7ZQwcFhtC2UzJFvaVi3mmtkgH2sIRRg6YseuBQToID6DxVMQgCDuIOXCIfeSq1kNUBQmGKPKRksMUaTt2fPjFdABxkQNzqZOeiSSIMuRQhLX1MwQsIO1BwAmhIOE4yIFBanWslqUuYi4cUB8x2KDyHU/FMQrj4BgWJ4hiRNVY7CHiIpcgT/kfZsotXV/tHSYlyLWRq4aCA4LzGceDET6iCg14wSLJZEXuTESLSiuaRxkvlnnBXXE+mIclj3nyQDxMgpujiuziiuBZ3hSDTFXnQ5O51tLlq2HExyKCouJaWQJCtzwC/7H0CpMkzlFpBcycm6Z8MZNBdi3yHEZl6Gd+yy95LlZnIJ2Va+uldRYfimUQyVDy+BOYiZpCTYiqpE4GdVJnXrFykCRpeH2fge2g1b9FmsCeMOlDWrYpIRQz24EQe2+uENvr+9T1vQFjBDNf+WIWcGX0Du4zQhlhju96nuuDEu6fuETMyuK2QsZXIivZn6bK6Qpe1cFFdpRE9alFIuP8mC/yZaoLNIizqcJ0GE8joanV4RNKneBmnKyuDafUzPXxfiFU+tAbGE+PkyhJEbgkUSCnRTs2rZZRO6ukbC1jawm7VJIMq+t4QLSEbsem1VKgdbO1AikuYWK7XEZmOtiozNZwaW0yqnBaxjK/LA9yGdwUSLGR/2k5H4O1FcPWp8TfaMrh/gP7GmaLVPAwmwmRf9niSrXDmMmxiKLrpqSKsaUgKahvzA4ML+dxSVAxxseb5HBHOdJRjnaUYx3lnI5ybkc5r6Oc31Fu0JXnzgrpqhHcVSW4q05wV6XgrlrBXdWCu+oFd1UM7qoZ0lUzpLOvdNUM6aoZ0lUzZKNmPiTVTUUVRbwnpUgtRYssmIlIJeokRmh2HaRJFOlIc9voB3ozupvqu40itPP7ZKlyN4TMsySdLyN+1Kiu1elzHeqLKhCOR2bWh2KfHj99BKtlIn0Pt8HR2gXDzgjQifURgNOcRdVpHkXJ3TUUI5JHp6HMk3T90kcoJz/KRVZXN78sofMBGpmKOvnyZZ4cJ/NFJHLRzAytTDC8ESls2FQYMWT5ZbLMTMlTlS2vhstMvOf57DAOP4gpsP+eq4o5h7RjROtsFsLW5zDQnC9SCVcp/5+QxszZUExTUWa/SD8tMUlXX7Wb9U7rtJ7qLE3mF/HtR6gnHmx1uF/iGWZBKheqbEFjKOFvGuSEMuNwAxA2xwH4DFAY28plrhLsJ8AXzKQYL2GSWzh/toxvlICIUcyDGYJy4SbbT0UwyzPN+Uzp6+o+lXyOLmGrsBZXCoB6+4pLqLwhFKr6bwVqyNTjKJPllf5BlStVzr5evUEHaPWf1/SN3hgY/FxA0ZnrimiyjPUWq/Jgop/kKGtCyfhn8I0H5UOtGbj8RIEEprWYcfWsp/YVMMom7Xq2f0wmmcjR6sDaUzHrHlrWuHyVhOu6msiVCB8aSF1i5VA038TAg06yeVHx6c5IhqHQNwWmnjEctNiIl3ORyqACyzUZsOCy3EiJaFuCyjrTUOTgBke4K0fMUIQfpaiMjZF6zIbmMjYD5nylSxM+ziBq5AJCjRBx/aDRbL0IsNhW+NRaUOH3jUao46mepr4UB6uUn8G5OyiCbFKE8j5wbu0icB+yMGwguHcSJqZXQxfAji76G47ZUOID8z+wZoX1z4z1v16hPcTfaB9AHZxg9iwn2KDjrn5QeIG7yQu+0uDboeIQF2wd4iJYdAkUMKpFUvlk6duHim6xgC9XMpI8ve8UJDba5mb7OiRleO1kTyD+Ba4auXH3yKKlN3Yjiz6TrGf738vytTEDHeGHKWiPPpqDvsqcNqegVpLZhp7uUI/bUMmOQj1pQ8U7CvW0BfXxGur7R3rWQrqrOj1vId1VRx21kO5q9D0i7ejr7SjW4zZWf0ehnrSh7mpUOm1B3dlM00K6qzo9byHdVUcdtZB+z+G3dQ94VN4Dvt6jG5/FtPIS3ZCXtnvC9u3QHNdoyFZojtto/JcGc1KDwVuBOWmDwS8N5rQG0x3IaRuI/dJAziog2ynlrIXlxXVyXkHZzlnOW1Be3FdGFZTtotioBeX/HsQ27u+idZ/Dvt/ksxlpK8+63zHUloFeVAbKtjLQi5aB1rS8lLN9FKu8fDXxt1+WSf738mXmf/8wx1YbWA6DrPUZWqpde5fzAk/e9Ud/GfA/qV/fy8/iqvgbBPM1oF18OVq/K3v0FR5Sr40c9RHJvQoqXjdayRqt62/JtiH3kfcaXcj9k5/U/wn8mnevFHd43aF4oWv8rroT+si7j5e21iznaf5efXxpuOh7HmWO5xE8IAPXI+aVpd1n7sD3HebbhDmDgfoC8HNVfHyZMbbG2H13xthfnjHFjccG8OMw22Wur76IU9bU98BhHduh2KMeYer7t66UXcosF2Vw/PUQ99AhgR/aQ0fQP4L+EfSPoX8M/WPon0D/BPon0D+F/in0T6F/Bv0z6J9B/xz659A/h/4I+iPoj+jvjyWQCDZgPdjN4xxj+2mWn/HJgP4MWH9Dap7HNs/WX/fsdXDUK56nclWRqFlU7CnWFFuKJcWOYmWEf++hXxXHilvFqeJScai4U5yNiJagBfO0YJoWzFLN5JepLDf1l+Zyv/l1k/4MvfgjtXf/A1BLBwgunXgWIAoAAFQ3AABQSwECFAAUAAgACAB9pbZCRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAH2ltkIunXgWIAoAAFQ3AAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAuAoAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | + | |
| − | <br /> | + | |
| − | | + | |
| − |
| + | |
| − | <div class="lueckentext-quiz">
| + | |
| − | | + | |
| − | Allgemein gilt:<br />
| + | |
| − | Betrachtet man den Term '''f''' (x - a), wird der Graph von f um '''a''' Einheiten auf der '''x''' - Achse verschoben.<br />
| + | |
| − | Für a < 0 wird der Graph nach '''links''', für a > 0 nach '''rechts''' verschoben.
| + | |
| − | | + | |
| | </div> | | </div> |
| − | <br />
| |
| | | | |
| | + | <div style="padding:1px;background:#1C86EE;border:0px groove;"> |
| | | | |
| − | <br />
| |
| | | | |
| − | === Verschiebung nach oben/unten === | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| | + | <tr><td width="800px" valign="top"> |
| | | | |
| − | Bearbeite nun den zweiten Abschnitt auf dem Arbeitsblatt:
| + | <big>Aber auch andere Funktionsgraphen lassen sich derartig verschieben.<br> |
| − | | + | |
| − | {|
| + | |
| − | | + | |
| − | |width="40%"|[[Datei:Verschiebung nach oben.png|400px]]
| + | |
| − | | + | |
| − | |width="3%"|
| + | |
| − | | + | |
| − | |valign="top"|Vergleiche auch hier die beiden Graphen bei: <br>
| + | |
| − | | + | |
| − | *g('''-1,5''') = -1,375 = f ('''-1,5''') + ____
| + | |
| | <br /> | | <br /> |
| − | *g(0) = ______ = f (___) + ____
| + | Im Folgenden wollen wir '''allgemein''' untersuchen, welchen Einfluss Parameter in einer Funktionsgleichung auf den Verlauf des Graphens der Funktion haben.<br> |
| | <br /> | | <br /> |
| − | *g(1) = _____________________________
| + | Arbeite dich entlang des [http://wikis.zum.de/projektwiki/Datei:AB_Verschieben.pdf Arbeitsblattes] zum Thema "Verschieben von Funktionsgraphen" durch die drei Unterkapitel!</big> |
| | | | |
| − |
| |
| − | Welcher Zusammenhang besteht zwischen den beiden Funktionen?<br>
| |
| − |
| |
| − | -> g(x) = f ( ______ ) _______
| |
| − |
| |
| − |
| |
| − | Für jeden x-Wert ist der Funktionswert von g gleich dem Funktionswert von f an der Stelle ________.
| |
| − |
| |
| − |
| |
| − | |}
| |
| − |
| |
| − | Kontrolliere dein Ergebnis mit den versteckten Lösungen:
| |
| | | | |
| | {| | | {| |
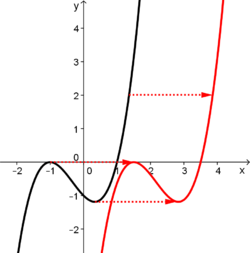
| − | | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|<big><center>Verschiebung in x- Richtung</center>]] |
| − | |width="40%"|<popup name="Graph"> | + | [[Datei:Verschiebung in x- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_Richtung]] |
| − | [[Datei:Verschiebung nach oben Lösung.png|400px]] | + | |
| − | </popup>
| + | |
| − | | + | |
| | |width="3%"| | | |width="3%"| |
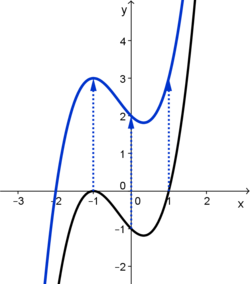
| − | | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in y- Richtung|<big><center>Verschiebung in y- Richtung</center>]] |
| − | |valign="top"|<popup name="Lösung"> | + | [[Datei:Verschiebung in y- Richtung.png|250px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_y-_Richtung]] |
| − | Vergleiche auch hier die beiden Graphen bei:<br>
| + | |
| − | | + | |
| − | *g(-1,5) = -1,375 = f (-1,5) + 2
| + | |
| − | <br />
| + | |
| − | *g(0) = 2 = f (0) + 2
| + | |
| − | <br />
| + | |
| − | *g(1) = 3 = f (1) + 2
| + | |
| − | | + | |
| − | | + | |
| − | Welcher Zusammenhang besteht zwischen beiden Funktionen?<br>
| + | |
| − | | + | |
| − | -> '''g(x) = f (x) + 2''' <br>
| + | |
| − | <br />
| + | |
| − | Für jeden x-Wert ist der Funktionswert von g gleich dem Funktionswert von f (x) + 2
| + | |
| − | </popup>
| + | |
| − | | + | |
| − | |} | + | |
| − | <br /> | + | |
| − | | + | |
| − | ==== Allgemein ====
| + | |
| − | | + | |
| − | | + | |
| − | | + | |
| − | Die Funktion g: x -> x³ + b lässt sich mittels des Parameters b nach oben und unten verschieben.<br>
| + | |
| − | Wenn du den Schieberegler auf b = 2 einstellst, erhälst du die obige Funktion g: x -> x³ + 2.<br>
| + | |
| − | <br>
| + | |
| − | Wie wirkt sich die Veränderung des Parameters b auf den Graphen von g aus?<br>
| + | |
| − | Was bewirkt ein positiver bzw. ein negativer Parameter b?
| + | |
| − | | + | |
| − | Beachte auch hier die '''Wertetabelle'''!
| + | |
| − | <br>
| + | |
| − | <br>
| + | |
| − | | + | |
| − | <ggb_applet width="648" height="619" version="4.2" ggbBase64="UEsDBBQACAAIAE6ltkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABOpbZCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b627bOBb+3XkKQj8WMxhfRN3dtTtI0lwGSGaLJlss9scCtETbnMiSR6Icu5i32jfYJ9tDUpIlK0mZS6dNksYUqUMenu9cRavjXzbLGK1plrM0mRh4YBqIJmEasWQ+MQo+6wfGL+9+GM9pOqfTjKBZmi0JnxjOwDJ286A3sD0xmUUTw40CPLJDr+9O6bTvzLDTJyPb6VMyinwS0Ci0ZwZCm5y9TdLfyJLmKxLSy3BBl+Q8DQmXay44X70dDm9ubgYV90GazYfz+XSwySMDwc6TfGKUF29hudakG1uSW6aJh/+6OFfL91mSc5KE1EBCqoK9++HN+IYlUXqDbljEFxPD8xwDLSibL0BM3woMNBREK5B1RUPO1jSHqY2ulJkvV4YkI4m4/0ZdobgWx0ARW7OIZhPDHPim4/mmbY3Up2+gNGM04SWtWfIcVquN14zeqGXFleTomGLemuVsGtOJMSNxDlKxZJYBorChrIBuzrcxnZKs6u/2g3vwCwTsMxVrAUsFAwDgBj1s4p5vmj3XLffSYGzdw7Xs79iWAzu+Zs+suFpNrjDeg4Ge3MoeR9ABT9NYLohBn+hPBI2lGhuhP+WFq/pO2fVU15cNNlWDy5uB+BiJjvckaXDPrqSxm9LA6j3x590hEW5wVZq5m+m+5mr8XGy38XPu4OY08DORK+W2TMtEPdFg1VjQeJ66ZaoxwFY2lmoc1biKxlHTHUXqKBpH0Tj2A+TrgGpVAuIWpL7fwyPvTiHxEzVZM3UbTF1wAfFP/nVY2g9yhY4HPoKjiE2Pd/lHMPTNlu1UhqNaXLb3wfBsmxoPqyA4LjeE8oWgLe2L02UutmiPpIUjjFwwY88Hg3QRHkHji4hhIewix4UuDpAnWh/ZIkg4yEYBEnTYRtKO3QA+HBlAPOTCWmLQV5EE2Q5ybYSl9TsIUEDSgwATywYK10UuTBLcsWBre8jxoGMHyIENCt/xRRyzYR70gbmFbIxsMRf7yPKQZyFf+B92hFt6gdg7LGohz0SemAoOCM6nHA9mBMgW0oAXrNKc1eAuaLyqtSJxZMmq4CV25Xi4jCocebpHHqXh9WENdnmHkpw3ySBV7RKiSl2tfPlmHJMpjaGquBSWgNCaxOA/huQwSxOOKitw1Ng8I6sFC/NLyjnMytHvZE3OCaebE6DOK96StUzjY1qEMYsYST6BmYglxIKozupOsMvqjldyCdM0iy63OdgO2vybZqkI4/5g1PiBaVt1x3Ktgdn8GYHphkQYvTNqzRm5MKm85ZrtSZWAdF2LRjY0r+CfZ8LrSmBF59f8MI13Q6uUJfyIrHiRyRINAm0mhDpI5jGV2Mr4CcVOeD1NN5cKVFutdbVdUZE/5Aam86M0TjOUCclgw/OynapW0oid1VSmpDElhVlpiUX1fTyyJIVsp6qVVKB2tbVSUlyJic2KDctltBGpreHT0mZE6VQkjJ9XHc7C61JSrOh/K5ZTMLdyWntJ/ExLjod7BjbOVxklUb6glH/Z5PxA7QvmzI5oHF82KUWQrQitEvrG6oBwsUwqgMo5Ab6PDmvSWZp0tiado0nnatJ5mnS+Jl2gSTfSxVlbIboawboqwbo6wbpKwbpawbpqwbp6wbqKwbqasXQ1Y2n7iq5mLF3NWLqase7VzMe0fqioo4h/J5V1CxWNRaZOE4QWl2GWxrGMNOvGdSg3Iy8z+bhRhnayTQuRvCFknqTZsojJYaO8FsOnMtSXZSD0z9Sq+2Sfbh8+BG45zT7Ag3DcuqHQOQPpaHsGyKlGUT1M4ji9uYRqhJH4OGI8zdq3rqCevGKrfFfe/FHAxUdoWEZ3yZcUPD1Kl6uYctqqQDqpYHxNM9ixqjESSPNFWuSq6KmnvRkXOf1A+OIgiT7SOcD/gYiamUPeUaS7dBbB3pcwUY2XeZWInP9PyGNqNKLzjFbpL5YHJirryrtms+LpDMulTrJ0+WuyvoKCYm+r42ElzzgPM7YSdQuaQhF/3UAnYjmBR4CoOQ+Ez0EKZVyccZFhP4F84YLRaQGLrGH8pEiuBQFNUELCBUqnNBkWCaeJhHwh1HWxzRhZonPYKHAiAn+oty8Ig8obIqGo/zaghFycR6kkL9QPmtyIcvbHzU9ogjb/+dH+SW4L7H1JoejksiCaFYncYF0dzORRjjAm2Mvv4Bp71cNOL3D7jvoILGu1IOKwZ+cqYJNN0OVq/5jNcsrRZmL0IWxsocGNuxdp1FbUjG1otG8duwKLQ818nQAMMsXyst6TF2csiqh8JlDVjIKgA0ZSLGnGwlrWqcQCGBbVRiqBHoePi1WJaToNiPC9EO1AqGJfLA7S0JKBOH1YZ0k2svQg0xyiAqcQSihNdkeJanNlAMWmkEAA7lryaitywEhcSXArcjA79hl8d89nb8Xaug9r4V3gvNIF4EljpQRG8HREVdCup64AAFnVNxyvoac9A58Y89K+5w37Rj+jqXok+4KRz59g5LcqUdvORSLdSnu/x9CfaNPdYHCAS7QOcAmXTiiAWR2YqrOjMljsbOPp0UDP30mxYTEj2VYrEODHggbSW1UE1TIpIP8CWM8ZOb8GVs8UNI/wftTsW7eGzSeZ0gOj5kPg0Rf1fVdU/EpFPe6IensufPmSnnQkfa06Pe1I+lod9awjqf1KJT3shqQXLGonKR/aZVLuWz7q317tdSCxuwnJrzB5WJH+lXRm3bPBl6e0+6uDrqzByxW1Y59HtX0Gdz2MdBDpmmfwPVnn+67GXmtCPO6I+oKLnI5tHle2qWWWxx2zNP9iq+wI8L52LqzrXO+7zoW/J+c66VjcC/atjsJOKoVp6+uko6/vSl2nHXW9puR1WqlLO3eddtT1XaWus466XnJd1dHXWaUvqIU1FXbWUdhfXgp3D9oqMQ7sx5zlHthPOqV8xHHutz186+B3RTe8Ot/92x9Fyv9efefzv/+qvtGFkcMko71CB8XWkfg3OOqV70blYL+z3Zec7DO9KN/VVi9NmeULdrsvSDjJ+AfxqhASJ+72wLWa7yC58vzdHgRB680kA32uc82X4bZacM9ruIXR6kN+y4mxPuRfzW6fCXXHbb0VVqKO26P+w2C3W7Bv9ZG+JUR8a+PeA6xvDuwWNq7nScycQfAwkJwWSBt9kJzvHiRv4HpNrw2UMwN2TsvHTeEUt2M2bH4rL1+gLP9/xbv/A1BLBwjgflmGUQkAAA8yAABQSwECFAAUAAgACABOpbZCRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAE6ltkLgflmGUQkAAA8yAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA6QkAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| + | |
| − | | + | |
| − | <br>
| + | |
| − | <br>
| + | |
| − | Kannst du die folgenden Graphen und Funktionsterme richtig zuordnen?
| + | |
| − | | + | |
| − | <div class="zuordnungs-quiz">
| + | |
| − | {|
| + | |
| − | | [[Datei:3x³+1.png|120px]] || f(x) = 3x³ + 1
| + | |
| − | |-
| + | |
| − | | [[Datei:X+3.png|120px]] || g(x) = x + 3
| + | |
| − | |-
| + | |
| − | | [[Datei:X² - 3.png|120px]] || h(x) = x² - 3
| + | |
| − | |-
| + | |
| − | | [[Datei:X³ + 5.png|120px]] || j(x) = x³ + 5
| + | |
| − | |-
| + | |
| − | | [[Datei:X⁴ - 2.png|120px]] || k(x) = x⁴ - 2
| + | |
| − | |}
| + | |
| − | | + | |
| − | </div>
| + | |
| − | | + | |
| − | === Verschiebung nach links/rechts und oben/unten ===
| + | |
| − | | + | |
| − | Jetzt widme dich dem dritten Abschnitt auf dem Arbeitsblatt!
| + | |
| − | | + | |
| − | {|
| + | |
| − | | + | |
| − | |width="40%"|[[Datei:Verschiebung nach rechts und oben.png|400px]]
| + | |
| − | | + | |
| | |width="3%"| | | |width="3%"| |
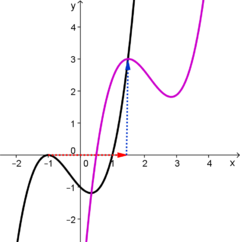
| − | | + | |valign="top"| [[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- und y- Richtung|<big><center>Verschiebung in x- und y- Richtung</center>]] |
| − | |valign="top"|Die Funktion j entsteht aus der Funktion f, die um ________________ nach rechts und _________________ nach oben verschoben wird.<br> | + | [[Datei:Verschiebung in x- und y- Richtung.png|240px|verweis=http://wikis.zum.de/projektwiki/Manipulationen_an_Funktionen/Verschieben_von_Funktionsgraphen/Verschiebung_in_x-_und_y-_Richtung]] |
| − | Vergleiche die beiden Graphen in einem charakteristischen Punkt:<br>
| + | |
| − | <br />
| + | |
| − | *j (3) = ____ = f (0) ______ = f (___ - ___) + ___
| + | |
| − | | + | |
| − | | + | |
| − | Im Funktionsterm von j äußert sich die Verschiebung wie folgt: <br>
| + | |
| − | | + | |
| − | -> j (x) = f ( __________)__________<br>
| + | |
| − | <br /> | + | |
| − | Für jeden x-Wert ist der Funktionswert von j gleich dem Funktionswert f (_____________).
| + | |
| − | | + | |
| | |} | | |} |
| − |
| |
| − |
| |
| − | Dein Ergebnis kannst du hier überprüfen:
| |
| | | | |
| | {| | | {| |
| − | | + | {{Vorlage:Lesepfad Ende |
| − | |width="40%"|<popup name="Graph"> | + | |Link zurück=[[Manipulationen an Funktionen|Zurück zur Übersicht]] |
| − | [[Datei:Verschiebung nach rechts und oben Lösung.png|400px]] | + | |Link vor=[[Manipulationen an Funktionen/Verschieben von Funktionsgraphen/Verschiebung in x- Richtung|Los geht´s mit der Verschiebung in x- Richtung]] |
| − | </popup>
| + | |Text Copyright=<colorize>Manipulationen an Funktionen</colorize> |
| − | | + | }} |
| − | |width="3%"| | + | |
| − | | + | |
| − | |valign="top"|<popup name="Lösung">
| + | |
| − | Die Funktion j entsteht aus der Funktion f, die um 3 Einheiten nach rechts und 2 Einheiten nach oben verschoben wird.
| + | |
| − | Vergleiche die beiden Graphen in einem charakteristischen Punkt:
| + | |
| − | <br>
| + | |
| − | | + | |
| − | *j (3) = 2 = f (0) + 2 = f (3 - 3) + 2
| + | |
| − | | + | |
| − | | + | |
| − | Im Funktionsterm von j äußert sich die Verschiebung wie folgt:<br>
| + | |
| − | | + | |
| − | -> '''j(x) = f (x - 3) + 2''' <br>
| + | |
| − | <br />
| + | |
| − | Für jeden x-Wert ist der Funktionswert von j gleich dem Funktionswert f (x - 3) + 2
| + | |
| − | </popup> | + | |
| − | | + | |
| | |} | | |} |
| − | <br />
| |
| − |
| |
| − | ==== Allgemein ====
| |
| − |
| |
| − |
| |
| − | In der Funktion j: x -> (x - a)³ + b werden beide Möglichkeiten der Verschiebung zusammengeführt.
| |
| − |
| |
| − | Wie wirkt sich die Veränderung von a und b auf den Graphen der Funktion j aus?
| |
| − |
| |
| − | Kannst du eine allgemeine Regel aufstellen?
| |
| − |
| |
| − | <ggb_applet width="737" height="619" version="4.2" ggbBase64="UEsDBBQACAAIAC6ltkIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAupbZCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b21LbSBq+zjxFly62klpsq3W0s3amgEAglcymQja1tRdb1ZbadgdZ8kgtMKl5q3mDebL9+6CDETFtyCwZk0C7W38fvu8/SoLxz+tlgq5oXrAsnVi4b1uIplEWs3Q+sUo+6w2tn1/9NJ7TbE6nOUGzLF8SPrG8vmM186DXdwMxmcUTa2TblEy9US+a+WHPm2HSI7YT96gdUJuM3NgPphZC64K9TLNfyJIWKxLRi2hBl+RdFhEu11xwvno5GFxfX/er3ftZPh/M59P+uogtBCdPi4mlP7yE5TYmXbtS3LFtPPj3+3dq+R5LC07SiFpIoCrZq5+eja9ZGmfX6JrFfDGxQt+10IKy+QJghs7QQgMhtAKsKxpxdkULmNrqSsx8ubKkGEnF9WfqE0pqOBaK2RWLaT6x7H5o45Hj2mGgf1ooyxlNuZa19Z6DarXxFaPXalnxSe7o2aMQVMAKNk3oxJqRpABULJ3lwCgcKC+hW/CbhE5JXvWb8+AD+AcC7CsVa8GWioaJ5QfOAcbhQWjbB76vz9La2Nmyq+432+qBZl/7wK52ddq7wvgBDBzIo9zaEXTAsyyRC2LQJ/oNQeOoxkXoN/nBV31PdwPVDWWDbdVgfXEofoxEJ3gUGnzgVmjcNhpY/UB8B99AhFu7Ks3sQmG1pY/xJoHeN7bzWgTayJfAHdux0YFosGocaIJAXbLVGJArG0c1nmp8JeOp6Z4S9ZSMp2Q89zEAnQogth0zgPiRaqw39NuOAPYv/svvzpbuTn7Qcb8H7Bh4j/H3B2wY2ht2UxmNarFut9Hw3Q41HlQRcKwPhIqFkNW2xemyEEd0R9K6EUY+mHAQgjH6CI+gCUW4cBD2kedDFw9RINoQuSJCeMhFQyTksIukDftD+OHJ6BEgH9YSg6EKI8j1kO8iLC3fQ8ACkt4DnDguSPg+8mGS2B2Lbd0AeQF03CHy4IDCb0IRxFyYB33Y3EEuRq6Yi0PkBChwUCh8D3vCJYOhODss6qDARoGYCs4HjqecDmYMkSvQgBessoLV5C5osqq1Inlk6arkmjs9Hi3jikee3RKPs+jyqCZbX6Gk4G0xyFNNNlR5ayNZPhsnZEoTKCkuhCUgdEUS8B9L7jDLUo4qK/DU2DwnqwWLigvKOcwq0BdyRd4RTtenIF1Ue8utZQ4f0zJKWMxI+hnMRCwhFkR1SnfDJqV7w5HaJcqyPL64KcB20Po/NM8g8Izs/qj1BYnnRl/x/Y0rIvcWERFG7402r4hJ37ikd6ZXNTKypkXF/jwXTqd5FZ3z4ihLmqFVxlJ+TFa8zGV5BjE2F5gO03lCJbUydEKhE11Os/WF4tRVa326WVGROuQBpvPjLMlylEtgIKDbqWqljDhZLWVLGVtK2JWSWFxfh3JGSsh2qlopBVpXR9NIcQUT29U2rJDBRmS1lktLkxFlU5ky/q7qcBZdaqRYyf9SLqdgbXra5pL4Oy05Htyyr3GxyimJiwWl/H6LG2qoMGd2TJPkoi2J3aCRdDT3reWB4nKZVgxVk+ytgrgWDO1tco6hnGso5xnK+YZygaFcaCg3NJQbGcph21TQVCPYVCXYVCfYVCnYVCvYVC3YVC/YVDHYVDOOqWYcY18x1YxjqhnHVDPOVs18zOpbijqMhN+UchopV2fggiYiVWcpQouLKM+SRIaaq+ozHDOSh5HDuYinVXAnN1kpsjcEzdMsX5YJOWrV12L4jQz2ug6E/pla9bbY57uHj2C3guYf4DY42big2DkDdHRzBuBUo6geJkmSXV9AOcJIchIznuWblz5BQfmJrYqmvvm1hA8foWE5bdIvKXl2nC1XCeV0owTpJIPxJc3hxKrISCHRl1lZqKqnnvZsXBb0A+GLwzT+SOdA/wciimYOmUeJNgkthrMvYaIa1+QTkfX/BZlMjcZ0ntMqASbycYnKu/Kq3S55OsNyqdM8W56nV5+gpLh11PGgwjMuopytROWCplDFX7bYiVlB4B4gbs8D8AWgUMbFGRc59jPgixaMTmmKrmD4tEwvxXXopiRaICgYLotBTqMFLyBRxygDyUGZcppKFSyE+t7f5Iws0Ts4OOxMuHyYgN4TBqU4REZREK5BKYV4OqXSvjAH0Oxa1LfP1y/QBK3/+9x9IY8J9r+kUIVyWSLNylQeuK4XZvLBjjAuOMsXcJVb9USjJ7j8jYoJLG21IOLRj127DthoWwlytX/OZgXlaC3d+WZi9Uati++zeFNvM7am8W1jaSouDjX0ZQosyIzLdQEoP5yxOKbyHkGVN4qBDhdpuaQ5i2qoRFIBG5bVQSo8u9JTlZ2KIB+3GMJbGWpI0HJFIp6qoSUDOD2IVUuyljGLTAsIEpxCZKE0bZ4rqsPVhZRAIPgOsC8+3YgcHIpPktxKHKyOfQVXNqDa2Ua18DVwZekQcOOxUngR3CxRFcLrqSvAL6v8lhuaqmn63dSkrFioR9wa2N4PoKahVpPjuVvV1Iq0T6inW2FoYi10FFqoKPR8jXqIvJCxCBkEo8U9waiF2tDdTANSz9EhqbpLvzsm3cm1WxHm3Bt/OoR90YR96RCG/o6mRqR9eVAEl+Zec7Zp/Oak2Zq0u51jG2nmMbvD2VxzNm+lOmO25g8zsS2hwpwtR7P1f7WwT3TNsWbsb7+WGf+HKBEm6z9+V707igQOU6zN+Y8gbdcqwawQkE/WoHpms6ZCZl/pe/2aTz1ys/Xj2Sbu3RmPkYy9OgJ4nhmnzganm/77x+/CHs35dR4Y9x7sw0/GsQoYYXgfx1DRHlZWe4i1o5vUs4d32Gr1RuTJjJWUa5Ywkt8YlbNbc/d2wzysrHJmFAwPH2h4+8GVW+VeM67cH9NJ/yy+ttbgR/h2Ed7z7qzCH+V6Oxbhu9BjDvW4C9XdU6ivu1CdPYV60oWK9xTqaQfq3TfMf32kbzpI91WnZx2k++qo5x2k+xp933aQ7mtKPXI6wTfYV6zHXazyCew+Yn3dxTrcU6gnXaj7mmtOO1D3tn7oIN1XnZ51kO6ro553kO5t+H3bgfpXzqqd5zVH1fOa5z3v3rcknZLD3VJymD6u+e6QjhtI7s6QjruQGtN+MkivG0jOzpBedyENnxzRSYMI74zopIsIPzmi0wbRbmhOO2jsJwfzpgazu3bedPA8vXLOajy7+89ZB8/Tu8/bGs/uUfttB88PELTPa0C7x+zzDqAfIGSLN5DuxtvMG/NXlw98K/JnvkEqOMn5B/HnBPKlY8/ue3jjjxuG6kVvfwi0fq19/n6SvA2S1uYkeT88ScN+YLe/fPWrCkCd0x4Wv8F9N2OD9q9Dyj9d0X/W+up/UEsHCAQhYtG2CQAAhjsAAFBLAQIUABQACAAIAC6ltkJFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgALqW2QgQhYtG2CQAAhjsAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABOCgAAAAA=" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| |
| − |
| |
| − | <br />
| |
| − | <br />
| |
| − |
| |
| − | Fülle den Lückentext mit den vorgegebenen Antwortmöglichkeiten aus.<br />
| |
| − | Ergänze anschließend die Lücken im Merksatz auf deinem Arbeitsblatt.<br />
| |
| − |
| |
| − |
| |
| − | <div class="lueckentext-quiz">
| |
| − | Allgemein gilt:<br />
| |
| − | Betrachtet man den Term '''f'''(x - a) + b, wird der Graph von f um '''a''' Einheiten auf der x - Achse und um '''b''' Einheiten auf der y - Achse verschoben.<br />
| |
| − | Für a < 0 wird der Graph nach '''links''', für a > 0 nach '''rechts''' verschoben.<br />
| |
| − | Der Parameter b < 0 verschiebt den Graphen nach '''unten''', b > 0 nach '''oben'''.
| |
| − |
| |
| − | </div>
| |