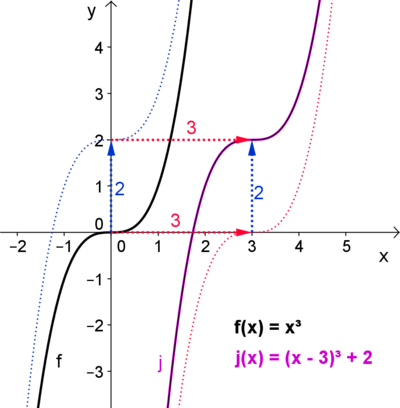
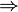Verschiebung in x- und y- Richtung
Aus Projektwiki - ein Wiki mit Schülern für Schüler.
|
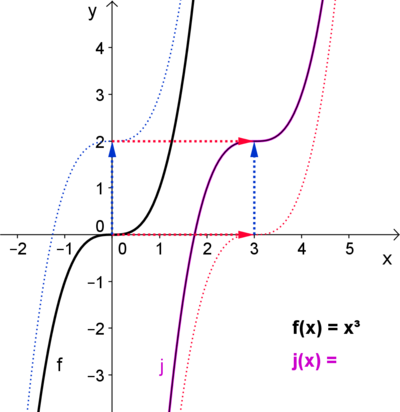
Jetzt widme dich dem dritten Abschnitt auf dem Arbeitsblatt!
|
|
Die Funktion j entsteht aus der Funktion f, die um ________________ nach rechts und _________________ nach oben verschoben wird.
Vergleiche die beiden Graphen in einem charakteristischen Punkt:
- j (3) = ____ = f (0) ______ = f (___ - ___) + ___
Im Funktionsterm von j äußert sich die Verschiebung wie folgt:
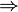 j (x) = f ( __________)__________ j (x) = f ( __________)__________
Für jeden x-Wert ist der Funktionswert von j gleich dem Funktionswert f (_________)______.
|
Dein Ergebnis kannst du hier überprüfen:
Ergänze auch hier die Längen der Pfeile und den Funktionsterm im Bild auf deinem Arbeitsblatt.
|
Allgemein
In der Funktion j: x -> (x - a)³ + b werden beide Möglichkeiten der Verschiebung zusammengeführt.
Wie wirkt sich die Veränderung von a und b auf den Graphen der Funktion j aus?
Kannst du eine allgemeine Regel aufstellen?
Fülle den Lückentext mit den vorgegebenen Antwortmöglichkeiten aus.
Ergänze anschließend die Lücken im Merksatz auf deinem Arbeitsblatt.
Allgemein gilt:
Betrachtet man den Term f(x - a) + b, wird der Graph von f um a Einheiten auf der x - Achse und um b Einheiten auf der y - Achse verschoben.
Für a < 0 wird der Graph nach links, für a > 0 nach rechts verschoben.
Der Parameter b < 0 sorgt für eine Verschiebung des Graphen nach unten, b > 0 nach oben.
|
Übung
Lies am Funktionsterm ab, wie weit der Graph der Funktionen ausgehend von f(x) jeweils in x- und in y- Richtung verschoben wird.
Gib als Extra-Aufgabe die Verschiebung der trigonometrischen Funktionen an.
Achte dabei auf die Vorzeichen!
Kannst du dir die Graphen der einzelnen Funktionen vorstellen?
|
|
Um deine Vorstellungskraft zu überprüfen, kannst du dir im Applet die Funktionsgraphen anzeigen lassen:
|
Manipulationen an Funktionen
|
|